NP-complete
계산 복잡도 이론 (Computational Complexity Theory) 에서, NP-complete 문제는 NP 중에서 가장 어려운 문제들이다 (그것들이 대부분 P 에는 속하지 않는다는 점에서). 그 이유는 만일 어떤 NP-complete 문제를 빨리 푸는 방법을 발견할 수 있다면, 모든 NP 문제들을 빨리 푸는데 그 알고리즘을 사용할 수 있기 때문이다. .........
현재 NP-complete 문제를 위한 모든 알려진 알고리즘들은 문제의 크기에서 지수적인 (exponential) 시간을 요구한다. 어떤 더 빠른 알고리즘이 있는지는 모른다. 그러므로 어떤 명백하지 않은 (non-trivial) 문제 크기의 NP-complete 를 해결하기 위해서, 다음과 같은 접근 방법중의 하나가 사용된다.
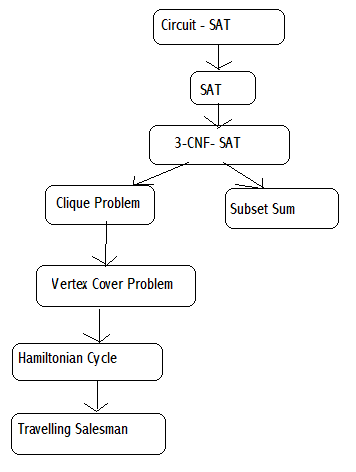
어떤 새로운 문제가 NP-complete 하다는 것을 증명하는 가장 쉬운 방법은, 이미 알려진 NP-complete 문제를 그것으로 환원하는 (reduce) 것이다. 그러므로 다양한 NP-complete 문제를 아는 것은 유익하다. 다음은 그중 일부이다.
다음 그림은 NP-complete 문제와 그들 사이의 상대적인 위치를 보여주는 그림이다. ......... (Wikipedia : NP-complete)

Stephen Cook 은 .... 1971 년 컴퓨팅의 이론을 주제로 열린 ACM (컴퓨팅 기계 협회) 의 제 3 차 연례 심포지엄에서 발표할 논문에서 .... 가능한 해법, 즉 '후보' 해법이 다항식 시간 내에 검토될 수 있는 문제들을 다루었다........ 어떤 프로그램은 그 해법을 추측해야만 하는 경우도 있다. 이러한 이유에서 쿡은 그 문제들에 비결정 다항식 (nondetermnistic polynomial) 혹은 NP 문제라는 이름을 붙였다. 추측 부분은 비결정적이고 검사 부분은 다항식이라는 의미이다. 세일즈맨의 여행 문제와 만족성 문제는 양자 모두 이러한 속성을 가진다. 여행 계획의 어떤 후보가 그 세일즈맨의 예산을 충족시키는지, 혹은 어떤 진리값 지정의 후보가 참인 공식을 만들어 낼 것인지를 빠른 시간 내에 적당한 후보를 찾아 내는 것이 과연 가능한가하는 것이다........
쿡의 논문이 발표되고 얼마 안 있어, UC 버클리의 Richard Karp 가 또 다른 21 가지 문제가 NP-완전임을 보여 주었다. 그 중엔 세일즈맨의 여행 문제와 긴밀하게 연관된 문제도 포함되어 있었다. ....... 카프의 연구 이후 세계 각지의 연구자들은 수천 가지의 문제가 NP-완전임을 보여 주었다. 전형적인 예는 전화망의 최적 기하학적 레이아웃, 또는 체커같은 게임을 하는 가장 좋은 방법 등이다. 쿡은 NP-완전 문제의 수에 당황하였다. "난 그저 NP-완전이 흥미로운 발상이라고만 생각하였습니다. 그것의 잠재적 영향력은 제대로 인식하지 못했던 것이지요." ...........

어떤 문제가 어느 정도의 시간 내에 해결될 수 있다면, 그것의 해법은 그 시간 내에 검토될 수 있다. 따라서, P 는 NP 내에 포함된다. 컴퓨터 과학에서 아직 미해결 상태인 이론상의 한 가지 큰 문제는, NP-완전에 속하는 천 가지 중요한 문제들이 실제로 다항식 시간 내에 해결될 수 있는지 아니면 지수 시간을 필요로 하는지 여부이다. 다시 말해, P 가 NP 와 일치하는가의 문제인 것이다.
스티븐 쿡 : 이 분야의 수학이 처해 있는 슬픈 상황은 우리가 이것들을 증명할 수 없다는 것입니다. 우리는 P 가 NP 와 일치하지 않는다는 것을 증명할 수가 없습니다. 따라서, 결국엔 누군가가 NP-완전 문제를 다항식 시간 내에 해결할 어떤 명쾌한 병렬 알고리즘을 고안해 낼 수 있을 것입니다. .... 사람들은 각기 다른 수많은 영역에서 그 문제를 공략하고 있습니다. 그리고 어찌되었든 P = NP 가 되는 것은 가능합니다. ........... (Dennis Shasha 1995)
term :
계산이론 (Theory of Computation) 계산 복잡도 이론 (Computational Complexity Theory) 비결정 완전 (NP-complete) 비결정 난해 (NP-hard) 다항식과 비결정다항식 (P and NP) 순회판매원 문제 (Travelling Salesman Problem)
site :
AI Topics : Traveling Salesperson and NP-complete Problems
paper :
NP-complete 의 정의 : Dennis Shasha
video :
P vs. NP and the Computational Compelxity Zoo : hackerdashery : 2014/08/26
The "P vs. NP" Problem : ETH Zurich : Avi Widgerson, 2012/05/07
23. Computational Complexity : MIT OCW : Erik Demaine, 2012/01/14 ... Playlist 47
NP Completeness∥& Reductions - Lecture 16 : Coderisland : Shai Simonson, 2012/19/31 .... Playlist 19