Proof
이산수학 :
Richard
Johnsonbaugh 저서, 강홍식.김정인.이도훈.이명재 번역, 교보문고, 1999
(원서 : Discrete Mathematics
6th ed, Prentice-Hall,
1997), Page 36~43
수학적 시스템 (mathematical system) 은 공리
(axioms), 정의 (definitions) 그리고 미정의 항 (undefined terms) 들로 구성된다.
공리는 참으로 간주한다. 정의는 존재하는 항목으로부터 새로운 개념을 만드는데
사용된다. 몇몇 항목들은 명쾌하게 정의되지 않아서 차라리 공리를 이용하여 정의한다.
수학적 시스템 내에서 정리를 유도할 수 있다. 정리 (theorem) 는 참으로 증명된
명제이다. 정리의 특별한 종류로 보조 정리와 추론이 있다. 보조 정리 (lemma) 는
자신이 옳다는 이야기가 너무나 당연한 정리이지만 다른 정리를 증명하는 데 사용된다.
당연한 결론 (corollary) 은 다른 정리를 빠르게 따르는 정리이다.
정리가 참으로 확정되는 논법을 증명 (proof) 이라
한다. 논리는 증명의 분석을 위한 도구이다. 이 절에서는 증명의 일반적인 방법을
기술하고 유효하거나 유효하지 않은 논의들을 분석하는 데 논리를 사용한다. 분해증명과
수학적 귀납법에서 특별한 증명 기술인 분해와 수학적 귀납법을 공부한다. 그러면
수학적 시스템의 몇 가지 예제부터 시작해 보자.
(예제
1)
유클리드 기하학은 수학적 시스템의 예를 제공한다.
공리들은 다음과 같다.
- 두 개의 다른 점이 주어졌을 때, 두 점을
잇는 한 개의 선이 실제로 존재한다.
- 한 개의 선과 선상이 아닌 곳에 한 개의
점이 주어졌을 때 그 점을 통과하면서 주어진 선과 평행인 선이 한 개 존재한다.
점과 선은 정의되지 않은 항목이며, 이들 성질을
기술하는 공리에 의해 함축적으로 정의되었다. 정의들은 다음과 같다.
- 대응하는 면과 대응하는 각이 같은 쌍으로
된 벡터들이라면 두 개의 삼각형은 합동 (congruent) 이다.
- 측정한 값의 합이 180 도라면 두 각은
보각 (supplementary) 이다.
(예제
2)
실수는 수학적 시스템의 다른 예를 제공한다.
공리들을 기술해 보자.
곱셉은 함축적으로 첫 번째 공리에 의해 정의되었으며,
다른 것들은 곱셈의 다른 성질들을 기술하는 것으로 추정된다.
정의들은 다음과 같다.
- (전술의 공리에서) P 의 원소는 양의
실수라 불린다.
- 실수
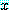 의 절대값
의 절대값 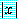 는
는 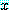 가 양의 정수, 0,
가 양의 정수, 0, 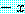 일 때
일 때 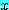 로 정의된다.
로 정의된다.
유클리드 기하학과 실수 시스템을 통하여 정리,
결론, 보조 정리의 몇가지 예를 보자.
(예제
3)
유클리드 기하학에서 정리의 예는
- 만약 삼각형의 두 변이 같다면 마주보고
있는 각도는 같다.
- 사변형의 대각선을 각각 2 등분한 점이
같으면 평행사변형이다.
(예제
4)
유클리드 기하학에서 결론의 예는
- 만약 삼각형의 두 변이 같으면 두 각이
같다.
이 결론은 예제 3 의 첫 번째 정리를 직관적으로
따른다.
(예제
5)
실수에 대한 정리의 예는
- 모든 실수
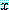 에 대하여
에 대하여 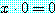 이다.
이다.
- 모든 실수
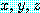 에 대하여 만약
에 대하여 만약 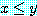 이면서
이면서 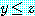 이면
이면 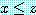 이다.
이다.
(예제
6)
실수에 대한 보조 정리의 예는
- 만약
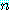 이 양의 정수이면
이 양의 정수이면  은 양의 정수이거나
은 양의 정수이거나 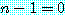 이다.
이다.
확실히 이 결과는 자신이 옳다는 것은 흥미가
없지만 다른 결과를 증명하는 데 유용하게 사용된다.
정리들은 가끔 다음 형태로 나타난다.
모든 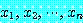 에 대하여 만약
에 대하여 만약 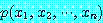 이면
이면 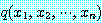 이다.
이다.
이 전체 정량 문장은 조건부 명제
만약 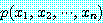 이면
이면 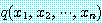 이다. (1)
이다. (1)
가 담화 영역에서 모든 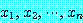 에 대하여 참으로 준비되면 참이다. 식 (1) 을 증명하기 위하여
에 대하여 참으로 준비되면 참이다. 식 (1) 을 증명하기 위하여 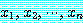 은 담화 영역에서 임의의 요소라고 가정한다. 만약
은 담화 영역에서 임의의 요소라고 가정한다. 만약 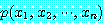 이 거짓이면 정의 1 에 의해서 식 (1) 은 참이므로 우리는
이 거짓이면 정의 1 에 의해서 식 (1) 은 참이므로 우리는 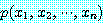 가 참일 경우만 고려하면 된다. 직접 증명 (direct proof) 은
가 참일 경우만 고려하면 된다. 직접 증명 (direct proof) 은 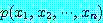 이 참이고 그리고 잘 알려진 공리, 정의, 먼저 처리된 정리를 이용하여 직접적으로
이 참이고 그리고 잘 알려진 공리, 정의, 먼저 처리된 정리를 이용하여 직접적으로
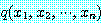 이 참이라고 보이도록 추정한다.
이 참이라고 보이도록 추정한다.
증명의 두 번째 기술은 반증에 의한 증명 (proof
by contradiction) 이다. 다른 공리들, 정의들, 그리고 이전에 유도된 정리들 뿐만
아니라 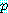 와
와  를 이용하여 가설
를 이용하여 가설 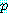 가 참이고 그 결론
가 참이고 그 결론  가 거짓이라는 추정에 의해 반증의 증명은 수립되었으며, 이를 이용하여 반증
(contradiction) 을 유도한다.
가 거짓이라는 추정에 의해 반증의 증명은 수립되었으며, 이를 이용하여 반증
(contradiction) 을 유도한다.
반증은 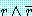 형태의 명제이다 (
형태의 명제이다 ( 은 임의의 명제). 반증에 의한 증명은
은 임의의 명제). 반증에 의한 증명은 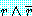 을 유도하여 식 (1) 이 참이라 결론 내리는 등, 반증에 의한 증명을 사용하여
식 (1) 이 수립되고부터 때때로 간접 증명 (indirect proof) 이라 불린다.
을 유도하여 식 (1) 이 참이라 결론 내리는 등, 반증에 의한 증명을 사용하여
식 (1) 이 수립되고부터 때때로 간접 증명 (indirect proof) 이라 불린다.
오직 하나의 차이점은 직접 증명의 가설과 반증에
의한 증명은 결론이 반대인 것이다. 직접 증명에서 반대되는 결론은 가정되지 않았으나,
반증에 의한 증명은 반대되는 결론이 가정된다.
반증에 의한 증명은 다음의 명제
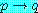 와
와 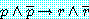
가 동치인 것이 알려져 정당화될 것이다. 진리표로부터
동치를 직접 확인한다.
|
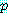
|

|

|
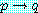
|
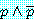
|
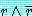
|
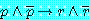
|
|
T
T
T
T
F
F
F
F
|
T
T
F
F
T
T
F
F
|
T
F
T
F
T
F
T
F
|
T
T
F
F
T
T
T
T
|
F
F
T
T
F
F
F
F
|
F
F
F
F
F
F
F
F
|
T
T
F
F
T
T
T
T
|
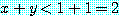
여기서 반증 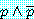 는
는
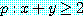
예제 8 에서 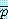 를 추정하기 위하여 식 (1) 의 반증에 의한 증명을 제안했고, 효과적으로
를 추정하기 위하여 식 (1) 의 반증에 의한 증명을 제안했고, 효과적으로
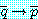 (2)
(2)
가 증명되었다.
반증에 의한 증명의 특별한 경우를 대우에 의한
증명 (proof by contrapositive) 이라 부른다. 증명의 단계에서 논법들은 정확히
(valid) 사용되어야 한다. 이 절의 남은 부분에서 확실한 논법의 개념을 연습하고,
이 개념의 좀더 상세한 부분을 탐구한다.
다음 명제들을 고려해 보자.
위의 문장들을 참이라고 가정하면 다음과 같은
이유 있는 결론을 내릴 수 있다.
일련의 명제들로부터 결론을 유도하는 과정을 연역적
추론 (deductive reasoning) 이라 한다. 식 (3) 과 같은 주어진 명제들은 가설 (hypotheses)
혹은 약속 (premises) 이라 하며 식 (4) 와 같이 가정에 따른 명제를 결론 (conclusion)
이라 한다. 연역적 논법 (deductive argument) 은 가설과 결론으로 구성된다. 수학과
컴퓨터 과학의 많은 증명들은 연역적 논법을 사용한다.
다음과 같은 형식의 어떤 논법이 있다고 하자.
논법 (5) 는 만약 가설 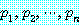 이 참이면 결론
이 참이면 결론  는 반드시 참인 것이 명백하다. 이 논의는 다음의 정의로 요약된다.
는 반드시 참인 것이 명백하다. 이 논의는 다음의 정의로 요약된다.
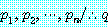 .
.
(예제
10)
다음의 논법이 명확한지를 결정하라.
|
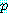
|

|
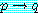
|
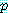
|

|
|
T
T
F
F
|
T
F
T
F
|
T
F
T
T
|
T
T
F
F
|
T
F
T
F
|
|
만약 2 = 3 이면, 내
목을 벤다.
내 목을 벤다.
|
|
∴ 2 = 3 이다.
|
또한 예제 10 의 진리표 실험에 의해서도 예제
11 의 논법 명백성을 결정할 수 있다. 표의 3 번째 행에서 가설이 참이고 결론이
거짓이므로, 논법은 명백하지 않다.
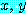 에 대하여,
에 대하여, 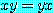 이다.
이다.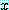 와
와 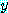 가 P 안에 있으면
가 P 안에 있으면 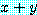 와
와 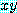 는 P 안에 있다.
는 P 안에 있다.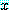 가 실수이면 정확하게 다음 문장들의 하나는 참이다.
가 실수이면 정확하게 다음 문장들의 하나는 참이다.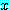 는 P 안에 있다
는 P 안에 있다  이다
이다 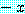 는 P 안에 있다.
는 P 안에 있다.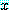 의 절대값
의 절대값 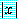 는
는 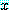 가 양의 정수, 0,
가 양의 정수, 0, 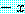 일 때
일 때 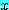 로 정의된다.
로 정의된다.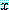 에 대하여
에 대하여 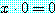 이다.
이다.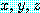 에 대하여 만약
에 대하여 만약 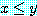 이면서
이면서 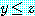 이면
이면 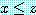 이다.
이다.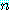 이 양의 정수이면
이 양의 정수이면  은 양의 정수이거나
은 양의 정수이거나 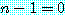 이다.
이다. 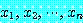 에 대하여 만약
에 대하여 만약 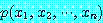 이면
이면 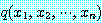 이다.
이다.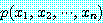 이면
이면 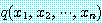 이다. (1)
이다. (1)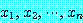 에 대하여 참으로 준비되면 참이다. 식 (1) 을 증명하기 위하여
에 대하여 참으로 준비되면 참이다. 식 (1) 을 증명하기 위하여 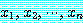 은 담화 영역에서 임의의 요소라고 가정한다. 만약
은 담화 영역에서 임의의 요소라고 가정한다. 만약 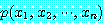 이 거짓이면 정의 1 에 의해서 식 (1) 은 참이므로 우리는
이 거짓이면 정의 1 에 의해서 식 (1) 은 참이므로 우리는 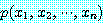 가 참일 경우만 고려하면 된다. 직접 증명 (direct proof) 은
가 참일 경우만 고려하면 된다. 직접 증명 (direct proof) 은 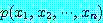 이 참이고 그리고 잘 알려진 공리, 정의, 먼저 처리된 정리를 이용하여 직접적으로
이 참이고 그리고 잘 알려진 공리, 정의, 먼저 처리된 정리를 이용하여 직접적으로
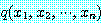 이 참이라고 보이도록 추정한다.
이 참이라고 보이도록 추정한다.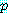

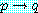
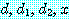 에 대하여
에 대하여 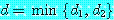 and
and 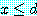 , then
, then 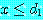 and
and 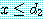
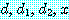 를 임의의 실수라고 하자. 앞에서
를 임의의 실수라고 하자. 앞에서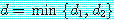 and
and 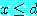
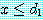 and
and 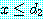
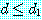 이며
이며 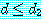 이다. 이전의 정리 (예제 5 의 두 번째 정리) 에 의하면
이다. 이전의 정리 (예제 5 의 두 번째 정리) 에 의하면 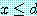 와
와 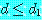 로부터
로부터 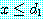 를 유도할 수 있다.
를 유도할 수 있다. 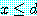 와
와 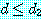 로부터도 같은 정리에 의해
로부터도 같은 정리에 의해 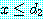 를 유도할 수 있다. 그러므로
를 유도할 수 있다. 그러므로 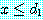 이며
이며 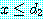 이다.
이다.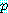 와
와  를 이용하여 가설
를 이용하여 가설 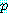 가 참이고 그 결론
가 참이고 그 결론  가 거짓이라는 추정에 의해 반증의 증명은 수립되었으며, 이를 이용하여 반증
(contradiction) 을 유도한다.
가 거짓이라는 추정에 의해 반증의 증명은 수립되었으며, 이를 이용하여 반증
(contradiction) 을 유도한다. 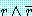 형태의 명제이다 (
형태의 명제이다 ( 은 임의의 명제). 반증에 의한 증명은
은 임의의 명제). 반증에 의한 증명은 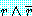 을 유도하여 식 (1) 이 참이라 결론 내리는 등, 반증에 의한 증명을 사용하여
식 (1) 이 수립되고부터 때때로 간접 증명 (indirect proof) 이라 불린다.
을 유도하여 식 (1) 이 참이라 결론 내리는 등, 반증에 의한 증명을 사용하여
식 (1) 이 수립되고부터 때때로 간접 증명 (indirect proof) 이라 불린다.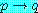 와
와 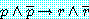
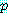


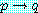
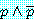
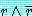
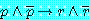
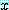 and
and 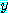 , if
, if 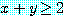 , then either
, then either 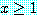 or
or 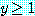
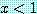 이며
이며 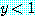 이다 (or 의 부정은 and 로 표시되는 논리를 위한 드모르간의 법칙 [예제 1.2.11]
을 상기하라). 이전의 정리를 이용하여 다음과 같은 등식을 구할 수 있다.
이다 (or 의 부정은 and 로 표시되는 논리를 위한 드모르간의 법칙 [예제 1.2.11]
을 상기하라). 이전의 정리를 이용하여 다음과 같은 등식을 구할 수 있다. 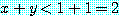
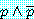 는
는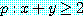
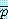 를 추정하기 위하여 식 (1) 의 반증에 의한 증명을 제안했고, 효과적으로
를 추정하기 위하여 식 (1) 의 반증에 의한 증명을 제안했고, 효과적으로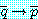 (2)
(2)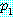 and
and 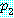 and ... and
and ... and 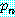 , then
, then  . (5)
. (5)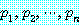 이 참이면 결론
이 참이면 결론  는 반드시 참인 것이 명백하다. 이 논의는 다음의 정의로 요약된다.
는 반드시 참인 것이 명백하다. 이 논의는 다음의 정의로 요약된다.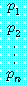
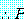
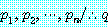 .
.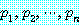 을 가설이라 하며 명제
을 가설이라 하며 명제  는 결론이라 한다. 논법은
는 결론이라 한다. 논법은 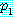 과
과 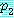 와
와 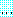 과
과 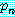 이 모두 참으로 준비되면
이 모두 참으로 준비되면  는 반드시 참이 되는 것이 명확하다. 그렇지 않으면 논법은 불명확하다 (허위).
는 반드시 참이 되는 것이 명확하다. 그렇지 않으면 논법은 불명확하다 (허위).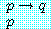
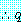
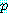

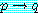
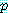

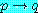 와
와 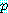 가 참인지 아니면 결론
가 참인지 아니면 결론  까지도 참인지를 얻을 수 있다. 그러므로 논법은 명확하다.
까지도 참인지를 얻을 수 있다. 그러므로 논법은 명확하다.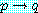 와
와 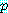 를 참이라 하자. 그러면
를 참이라 하자. 그러면 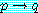 가 거짓인 것 이외에는
가 거짓인 것 이외에는  는 참이 틀림없다. 그러므로 논법은 명백하다.
는 참이 틀림없다. 그러므로 논법은 명백하다.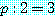 ,
, 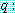 내 목을 벤다.
내 목을 벤다.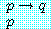
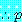
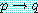 와
와  는 함께 참이거나
는 함께 참이거나 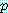 가 참이어야 한다.
가 참이어야 한다. 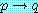 와
와  를 함께 참이라 하자.
를 함께 참이라 하자. 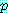 는 거짓이며
는 거짓이며  는 참이 될 수 있다. 이 경우
는 참이 될 수 있다. 이 경우 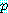 는 참이 아니며 논법은 명백하지 않다.
는 참이 아니며 논법은 명백하지 않다.