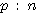 은 홀의 정수이다. (1)
은 홀의 정수이다. (1)
Quantifier
이산수학 : Richard Johnsonbaugh 저서, 강홍식.김정인.이도훈.이명재 번역, 교보문고, 1999 (원서 : Discrete Mathematics 6th ed, Prentice-Hall, 1997), Page 19~34
명제절과 조건 명제와 논리적 동치절의 논리에서는 컴퓨터 과학과 수학의 문장 대부분을 묘사하기는 어려운 명제를 다루었다.
예를 들어, 다음 문장을 보자.
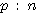 은 홀의 정수이다. (1)
은 홀의 정수이다. (1)
명제는 참이거나 거짓인 문장이다. 문장 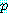 는
는 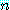 의 값에 의하여 참이거나 거짓이 결정되기 때문에 명제가 아니다. 예를 들어,
의 값에 의하여 참이거나 거짓이 결정되기 때문에 명제가 아니다. 예를 들어,
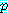 는
는 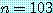 이면 참이며, 만약
이면 참이며, 만약  이면 거짓이다. 컴퓨터 과학과 수학 문장들의 대부분은 변수를 사용되기 때문에
다음 문장들을 포함하는 논리 시스템으로 확장해야 한다.
이면 거짓이다. 컴퓨터 과학과 수학 문장들의 대부분은 변수를 사용되기 때문에
다음 문장들을 포함하는 논리 시스템으로 확장해야 한다.
(정의 1)
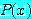 를 집합
를 집합 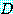 와 변수
와 변수 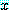 를 포함하는 문장이라 하자. 만약
를 포함하는 문장이라 하자. 만약 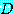 에 각각의
에 각각의 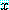 가 포함되면
가 포함되면 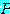 를 명제 함수 (propositional function) 라고 부르며 (
를 명제 함수 (propositional function) 라고 부르며 (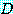 에 관해서는),
에 관해서는), 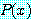 는 명제이다. 여기서
는 명제이다. 여기서 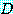 를
를 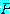 의 담화 영역 (domain of discourse) 이라고 부른다.
의 담화 영역 (domain of discourse) 이라고 부른다.
(예제 2)
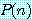 문장을
문장을
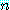 은 홀의 정수이다.
은 홀의 정수이다.
라고 하자.
그리고 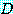 는 양의 정수 집합이다. 그러면 각각의
는 양의 정수 집합이다. 그러면 각각의 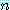 이
이 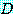 속에 있기 때문에
속에 있기 때문에 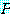 는 담화 영역
는 담화 영역 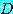 를 가진 명제 함수이며
를 가진 명제 함수이며 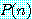 은 명제이다 (
은 명제이다 (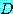 에 속해있는 각각의
에 속해있는 각각의 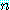 에 대하여
에 대하여 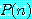 은 참이거나 거짓이지만 둘 다는 아니다). 예를 들어, 만약
은 참이거나 거짓이지만 둘 다는 아니다). 예를 들어, 만약  이면 우리는 다음 명제를 얻는다.
이면 우리는 다음 명제를 얻는다.
1 은 홀수다.
(참인 명제). 만약  이면 우리는 다음 명제를 얻는다.
이면 우리는 다음 명제를 얻는다.
2 는 홀수이다.
(거짓인 명제).
명제 함수 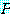 에서 자기 자신은 참도 거짓도 아니다. 그러나 각각의
에서 자기 자신은 참도 거짓도 아니다. 그러나 각각의 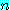 이 그것의 담화 영역에 속해 있으므로,
이 그것의 담화 영역에 속해 있으므로, 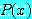 는 명제이고 따라서 참 또는 거짓 중 하나다. 우리는 담화 영역의 각 요소가
하나의 명제의 분류로 정의되는 것과 같은 명제 함수를 생각할 수 있다. 예를 들어,
만약
는 명제이고 따라서 참 또는 거짓 중 하나다. 우리는 담화 영역의 각 요소가
하나의 명제의 분류로 정의되는 것과 같은 명제 함수를 생각할 수 있다. 예를 들어,
만약 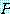 가 양의 정수 집합으로 설정해 놓은 담화 영역을 가진 명제 함수라면 우리는
명제 분류
가 양의 정수 집합으로 설정해 놓은 담화 영역을 가진 명제 함수라면 우리는
명제 분류
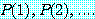
를 얻는다. 각각의 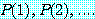 는 참, 거짓 중 하나다.
는 참, 거짓 중 하나다.
(예제 3)
다음은 명제 함수이다.
(a) 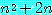 은 홀의 정수 (담화 영역 = 양의 정수 집합)
은 홀의 정수 (담화 영역 = 양의 정수 집합)
(b) 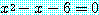 (담화 영역 = 실수 집합)
(담화 영역 = 실수 집합)
(c) 야구 선수가 1974 년에 3 할 이상의 안타를 쳤다 (담화 영역 = 야구 선수의 집합).
(d) 그 음식점은 시카고 잡지에 별 2 개 이상으로 평가되었다 (담화 영역 = 시카고 잡지에 평가된 음식점의 집합).
(a) 문장에서 각각의 양의 정수 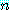 에 의해 우리는 명제를 얻는다. 그러므로 문장 (a) 는 명제 함수이다.
에 의해 우리는 명제를 얻는다. 그러므로 문장 (a) 는 명제 함수이다.
마찬가지로 문장 (b) 에서는 각각의 실수 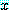 에 의해 명제를 얻는다. 그러므로 문장 (a) 는 명제 함수이다.
에 의해 명제를 얻는다. 그러므로 문장 (a) 는 명제 함수이다.
"야구 선수" 처럼 문장 (c) 에서는 변수를 생각할 수 있다. 우리는 언제든지 변수 "야구 선수" 자리에 특별한 야구 선수를 대신하여 쓸 수 있다. 예를 들어, 만약 우리가 "야구 선수" 에 "Wilie Stargell" 을 대신해서 쓴다면, 문장 (c) 는
Wilie Stargell 는 1974 년에 3 할 이상의 안타를 쳤다.
가 되고, 이것은 참이다. 만약 우리가 "야구 선수" 대신에 "Carlton Fisk" 를 썼다면 문장 (c) 는
Carlton Fisk 는 1974 년에 3 할 이상의 안타를 쳤다.
가 되며, 이것은 거짓이다. 그러므로 문장 (c) 는 명제 함수이다.
문장 (d) 는 문장 (c) 와 형식이 비슷하다: 여기서는 "음식점" 이 변수에 해당한다. 언제든지 우리는 변수 "음식점" 에 시카고 잡지에 평가된 음식점을 대신 쓸 수 있다. 그 문장은 명제이다. 예를 들어, 만약 "음식점" 에 "Yugo Inn" 을 대입한다면 문장 (d) 는
Yugo Inn 은 시카고 잡지에 별 2 개 이상으로 평가되었다.
가 되며, 이것은 거짓이다. 만약 "음식점" 에 "Le Francais" 를 대신하였다면 문장 (d) 는,
Le Francais 는 시카고 잡지에 별 2 개 이상으로 평가되었다.
이고, 이것은 참이다. 문장 (d) 는 명제 함수이다.
컴퓨터 과학과 수학에서 문장의 대부분은 "모든 것에 대하여" 와 "일부분에 대하여" 와 같은 표현이 들어간다. 예를 들면, 수학에서 우리는 다음과 같은 정리를 볼 수 있다.
모든 삼각형 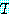 에서,
에서, 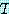 의 내각의 합은 180 도로 동일하다.
의 내각의 합은 180 도로 동일하다.
컴퓨터 과학에는 다음과 같은 정리가 있다.
일부분의 프로그램 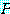 는
는 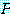 의 출력이
의 출력이 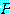 그 자신이다.
그 자신이다.
우리는 이제 "모든 것에 대하여" 와 "일부분에 대하여" 를 포함하는 문장을 조절할 수 있도록 명제절과 조건 명제와 논리적 동치절의 논리적 시스템을 확장시킨다.
(정의 4)
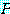 는 담화 영역
는 담화 영역 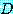 를 가진 명제 함수라 하자. 다음의 문장
를 가진 명제 함수라 하자. 다음의 문장
for every 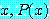
는 전체적으로 정량화된 문장이라 한다. 부호 ∀ 는 "모든 것에 대하여 (for every)" 를 의미한다.
즉, 문장
for every 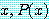
는 이렇게 쓰여진다.
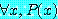 .
.
부호 ∀ 를 전체 정량자 (universal quantifier) 라고 한다.
문장
for every 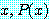
는 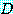 안의 모든
안의 모든 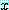 에 대하여 함수
에 대하여 함수 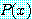 가 참이면 참이다. 문장
가 참이면 참이다. 문장
for every 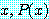
는 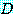 안의
안의 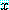 중, 적어도 하나의
중, 적어도 하나의 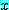 에 대하여 거짓이면
에 대하여 거짓이면 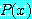 는 거짓이고, 따라서 문장은 거짓이다. 문장
는 거짓이고, 따라서 문장은 거짓이다. 문장
for some 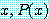
는 존재적 정량화 문장이라고 한다. 기호 ∃ 는 "일부분에 대하여" 를 의미한다.
따라서 다음 문장
for some 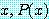
는
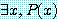
로 쓸 수 있다.
∃ 를 존재 정량자 (existential quantifier) 라 한다.
문장
for some 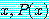
는 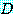 속의 적어도 하나의
속의 적어도 하나의 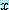 에 대하여
에 대하여 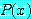 가 참이면 위 문장은 참이다. 또한 문장
가 참이면 위 문장은 참이다. 또한 문장
for some 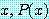
는 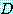 에서 모든
에서 모든 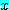 에 대하여
에 대하여 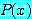 가 거짓이면 거짓이다.
가 거짓이면 거짓이다.
명제 함수 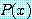 에서 변수
에서 변수 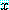 를 자유 변수라고 한다 (자유라는 말은 담화 영역 안을 자유롭게 배회한다는
뜻에서 유래했다). 변수
를 자유 변수라고 한다 (자유라는 말은 담화 영역 안을 자유롭게 배회한다는
뜻에서 유래했다). 변수 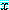 는 전체 정량화된 문장에서
는 전체 정량화된 문장에서
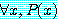 (2)
(2)
또는 존재 정량화된 문장에서는
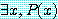 (3)
(3)
라고 적으며 한계 변수 (bound variable) 라고 부른다 (한계라는 말은 정량자 ∀ 와 ∃ 를 사용한다는 이유에서 유래했다). 이전에 명제 함수는 진리값을 가지지 않는다는 것을 지적했다. 반면에 정의 4 는 정량화된 문장 (2) 와 (3) 에 진리값을 할당한다. 결론은 자유 변수를 포함한 선언은 명제가 아니고 자유 변수를 포함하지 않은 선언은 명제이다.
다른 표기 방법으로
for every 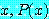
는
for all 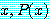
이며
for any 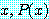
이다.
기호 ∀ 는 "for every", "for all", 또는 "for any" 로 읽는다.
또한 다른 표기 방법으로
for some 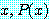
는
for at least on 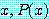
이며
there exists 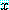 such that,
such that, 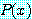
이다. 기호 ∃ 는 "for some", "for at least one", 또는 "there exists" 로 읽는다.
때때로 담화 영역 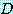 를 조건으로 하면, 전체적으로 정량화된 문장은
를 조건으로 하면, 전체적으로 정량화된 문장은
for every 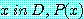
이며, 존재 정량화된 문장은
for some 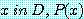
이다.
(예제 5)
문장
for every real number 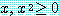
는 전체 정량화된 문장이다. 담화 영역은 실수로
구성된다. 위의 문장은 참이다. 왜냐하면 모든 실수에 대하여 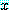 의 제곱의 양수이거나 영이기 때문이다.
의 제곱의 양수이거나 영이기 때문이다.
(예제 6)
전체 정량화된 문장
for every real number 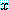 , if
, if 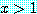 , then
, then 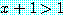
는 참이다. 이때 다음의 문장
if 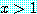 , then
, then 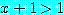
는 모든 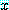 에 대해 참이 됨을 검사해야 한다.
에 대해 참이 됨을 검사해야 한다.
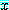 를 어떤 실수라고 하자. 어떤 실수에 대하여도
를 어떤 실수라고 하자. 어떤 실수에 대하여도 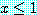 든지
든지 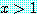 이면 참이다.
이면 참이다.
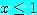 일 경우는 조건부 명제
일 경우는 조건부 명제
if 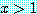 , then
, then 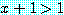
가 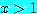 라는 가설이 거짓이기 때문에 참이다 (가정이 거짓일 때, 조건부 명제는 결론이
참이건 거짓이건 관계없이 참이었음을 기억하라).
라는 가설이 거짓이기 때문에 참이다 (가정이 거짓일 때, 조건부 명제는 결론이
참이건 거짓이건 관계없이 참이었음을 기억하라).
이제 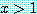 이라고 가정해 보자.
이라고 가정해 보자. 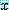 의 특정값을 고려하지 않아도
의 특정값을 고려하지 않아도 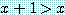 이다.
이다.
그러면
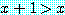 and
and 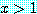
로부터 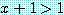 로 결론 내리며, 따라서 결론은 참이다.
로 결론 내리며, 따라서 결론은 참이다.
만약 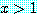 이면, 가정과 결론은 둘 다 참이다. 그러므로 조건 명제
이면, 가정과 결론은 둘 다 참이다. 그러므로 조건 명제
if 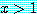 then
then 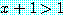
는 참이다.
우리는 모든 실수에 대하여, 명제
if 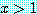 then
then 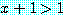
는 참이라는 것을 보였다. 그러므로 모든 실수에 대하여, 전체 정량화된 문장
for every real number 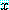 , if
, if 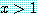 then
then 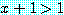
에 대하여 조건부 명제
if 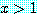 then
then 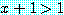
가 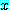 의 값에 관계없이 참이라면, 문장은 참이다. 특별한 경우로
의 값에 관계없이 참이라면, 문장은 참이다. 특별한 경우로 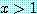 가 거짓이라면,
가 거짓이라면,
명제
if 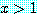 then
then 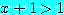
는 참이다.
정의 4 에 따라서 전체 정량적인 문장
for every 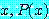
는 담화 영역 속의 적어도 하나의 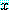 에 대하여 거짓이면
에 대하여 거짓이면 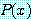 는 거짓이다.
는 거짓이다. 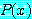 를 거짓으로 만드는 담화 영역 속의
를 거짓으로 만드는 담화 영역 속의 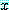 의 값을 문장
의 값을 문장
for every 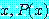
의 반례 (counterexample) 라 한다.
(예제 7)
전체 정량 문장
for every real number 
는 만약  일 때 명제
일 때 명제
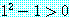
는 거짓이 되어, 원래 문장을 거짓으로 만든다. 즉, 값 1 은 다음 문장
for every real number 
의 반례이다.
전체 정량 문장
for every 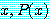
가 거짓이 되는 것을 보여 보자. 명제 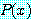 를 거짓으로 만들기 위해서는 담화 영역 속의
를 거짓으로 만들기 위해서는 담화 영역 속의 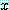 값이 하나만 거짓이면 충분하다.
값이 하나만 거짓이면 충분하다.
for every 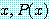
문장의 반례를 드는 방법은 문장의 참을 증명할 때 사용하는 방법과는 상당히 다르다.
다음 문장
for every 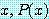
의 참을 증명하기 위해서는 담화 영역 내의 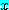 의 모든 값에 대하여 for every
의 모든 값에 대하여 for every 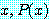 가 참임을 보여야 한다.
가 참임을 보여야 한다.
(예제 8)
전체 정량 문장
모든 양의 정수 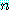 에 대하여, 만약
에 대하여, 만약 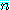 이 짝수이면
이 짝수이면 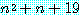 는 소수이다.
는 소수이다.
는 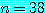 일 때 반증을 얻을 수 있으므로 거짓이다. 조건부 명제
일 때 반증을 얻을 수 있으므로 거짓이다. 조건부 명제
만약 38 이 짝수이면 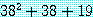 는 소수이다.
는 소수이다.
는 가정
38 이 짝수,
는 참이지만, 결론
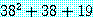 는 소수,
는 소수,
가 거짓이다. 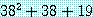 는 다음과 같이 인수 분해되기 때문에 소수가 아니다.
는 다음과 같이 인수 분해되기 때문에 소수가 아니다.
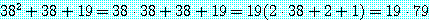
존재 정량 문장으로 돌아가 보자. 정의 4 에 따라서 존재 정량 문장
for some 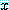 in
in 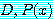
는 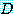 속의
속의 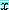 에 대하여 적어도 하나가 참이면
에 대하여 적어도 하나가 참이면 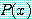 는 참이다. 만약
는 참이다. 만약 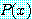 가 어떤 값
가 어떤 값 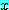 에 대하여 참이면
에 대하여 참이면 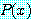 가 다른 어떤 값
가 다른 어떤 값 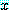 에 대하여 거짓이어도
에 대하여 거짓이어도 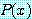 는 참이 확실히 가능하다.
는 참이 확실히 가능하다.
(예제 9)
존재 정량 문장
for some real number 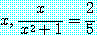
는 적어도 하나의 실수 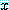 에 대하여
에 대하여
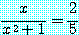
가 참이 될 수 있으므로 참이다. 예를 들어,
 일 때 우리는 참인 명제를 얻게 된다.
일 때 우리는 참인 명제를 얻게 된다.
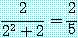
이것은 모든 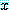 값의 경우에 참의 명제가 되는 것은 아니다. 예를 들면, 다음 명제
값의 경우에 참의 명제가 되는 것은 아니다. 예를 들면, 다음 명제
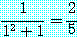
는 거짓이다.
(예제 10)
존재 정량 문장
어떤 양의 정수 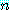 에 대하여, 만약
에 대하여, 만약 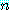 이 소수이면,
이 소수이면,
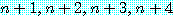 는 소수가 아니다,
는 소수가 아니다,
는 우리가 조건부 명제
만약 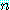 이 소수이면,
이 소수이면, 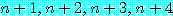 는 소수가 아니다,
는 소수가 아니다,
를 참으로 만드는 적어도 하나의 정수 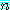 을 찾을 수 있기 때문에 참이다. 예를 들면,
을 찾을 수 있기 때문에 참이다. 예를 들면, 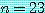 일 때, 우리는 참인 명제를 얻을 수 있다.
일 때, 우리는 참인 명제를 얻을 수 있다.
만약 23 이 소수이면 24, 25, 26, 27 은 소수가 아니다.
(이 조건부 명제는 가장 "23 은 소수이다."
와 결론 "24, 25, 26, 그리고 27 은 소수가 아니다." 가 모두 참이기
때문에 참이다). 몇몇 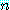 의 값은 조건부 명제를 참으로 만든다 (예를 들면,
의 값은 조건부 명제를 참으로 만든다 (예를 들면,  ) 하지만 다른 것들은 그것을 거짓으로 만든다 (예를 들면,
) 하지만 다른 것들은 그것을 거짓으로 만든다 (예를 들면, 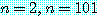 ). 요점은 우리가 조건부 명제
). 요점은 우리가 조건부 명제
만약 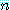 이 소수이면,
이 소수이면, 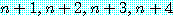 는 소수가 아니다.
는 소수가 아니다.
를 참으로 만드는 하나의 값을 찾는 것이다. 따라서 존재 정량 문장
어떤 양의 정수 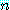 에 대하여, 만약
에 대하여, 만약 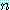 이 소수이면,
이 소수이면,
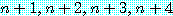 는 소수가 아니다,
는 소수가 아니다,
는 참이다.
정의 4 에 따라서 존재 정량 문장
for some 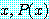
는 담화 영역에 모든 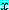 에 대하여 명제
에 대하여 명제 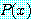 가 거짓이어야 거짓이 된다.
가 거짓이어야 거짓이 된다.
(예제 11)
다음 존재 정량 문장을 살펴보자.
for some real number 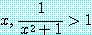
은 거짓이다. 이를 증명하려면
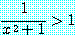
가 모든 실수 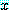 의 경우 거짓이라는 것을 보여야 한다. 또한
의 경우 거짓이라는 것을 보여야 한다. 또한
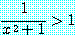
는
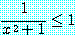
이 정확히 참일 때 거짓이다. 그러므로,
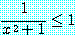
가 모든 실수 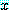 에 대하여 참이라는 것을 보여야 한다.
에 대하여 참이라는 것을 보여야 한다. 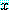 를 임의의 실수라 하자.
를 임의의 실수라 하자. 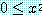 로부터 부등식의 양변에 1 을 더하여
로부터 부등식의 양변에 1 을 더하여 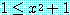 을 얻을 수 있다. 마지막으로
을 얻을 수 있다. 마지막으로 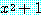 로 부등식의 양변을 나누면
로 부등식의 양변을 나누면
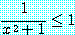
를 얻을 수 있다. 그러므로 문장
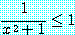
는 모든 실수 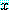 에 대하여 참이다. 그러므로 문장
에 대하여 참이다. 그러므로 문장
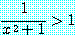
는 모든 실수 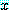 에 대하여 거짓이다. 이로서 존재 정량 문장
에 대하여 거짓이다. 이로서 존재 정량 문장
for some 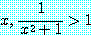
는 거짓이다.
예제 11 에서 존재 정량 문장은 전체 정량 문장이 참이라는 것이 판명된 것과 관련되어서 거짓이다. 따름 정리 (following theorem) 는 이러한 관계를 정확히 만든다. 이 정리는 드모르간의 논리 법칙을 일반화한다 (예제 11).
(정리 12) 드모르간의 논리 법칙 일반화
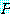 가 명제 함수라면 (a) 와 (b) 에 있는 명제의 각 쌍은 같은 진리값을 갖는다
(즉, 양쪽 다 참이거나 양쪽 다 거짓이다).
가 명제 함수라면 (a) 와 (b) 에 있는 명제의 각 쌍은 같은 진리값을 갖는다
(즉, 양쪽 다 참이거나 양쪽 다 거짓이다).
(a) 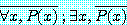
(b) 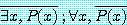
증명 - part (a) 만 증명하고, part (b) 의 증명은 독자에게 남긴다 (연습문제 50).
명제 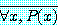 가 참이라고 가정하자. 그러면 명제
가 참이라고 가정하자. 그러면 명제 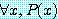 는 거짓이다. 정의 4 에 의해, 명제
는 거짓이다. 정의 4 에 의해, 명제 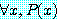 는
는 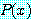 가 담화 영역에서 적어도 하나의
가 담화 영역에서 적어도 하나의 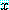 가 거짓이라면
가 거짓이라면 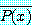 는 담화 영역에서 적어도 하나의
는 담화 영역에서 적어도 하나의 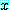 가 참이다. 다시 정의 4 에 의해
가 참이다. 다시 정의 4 에 의해 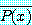 가 담화 여역에서 적어도 하나의
가 담화 여역에서 적어도 하나의 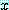 가 참일 때, 명제
가 참일 때, 명제 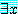 ,
, 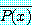 는 참이다. 그러므로 명제
는 참이다. 그러므로 명제 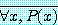 가 참이라면, 명제
가 참이라면, 명제 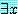 ,
, 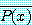 는 참이다. 같은 식으로 명제
는 참이다. 같은 식으로 명제 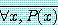 가 거짓이라면, 명제
가 거짓이라면, 명제 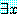 ,
, 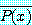 도 거짓이다.
도 거짓이다.
그러므로 part (a) 의 명제 한 쌍은 항상 같은 진리값을 가진다.
(예제 13)
문장 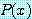 를
를
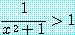
라 하자. 예제 11 에서
for some real number 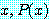
는
for every real number 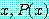 (4)
(4)
가 참임을 밝히므로 거짓임을 보였다.
이 기법은 정리 12 에서 매력적으로 사용되었다. 다음으로 부정 (4)
|
for every real number |
이 거짓이라고 결론내려서 명제 (4) 가 참인 것을 밝힌다. 정리 12 에 의해서, part (a) 는
for some real number 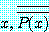
혹은 동치
for some real number 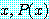
또한 거짓이다.
전체 정량 명제는 개별 명제 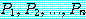 의 복합 명제
의 복합 명제
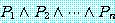 (5)
(5)
를 일반화한 것이고 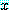 가 담화 영역의 일원일 때, 정해지지 않은
가 담화 영역의 일원일 때, 정해지지 않은 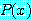 의 구성원을 재배치하여 만들었으며, 따라서 (5) 를
의 구성원을 재배치하여 만들었으며, 따라서 (5) 를
for every 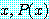 (6)
(6)
와 같이 쓸 수 있다.
명제 (5) 는 모든 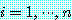 에서 오직
에서 오직 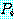 가 참이라면 참이다. 명제 (6) 의 진리값은 유사하게 정의된다. (6) 은 오직
담화 영역에서 모든
가 참이라면 참이다. 명제 (6) 의 진리값은 유사하게 정의된다. (6) 은 오직
담화 영역에서 모든 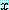 에 대하여 참이라면
에 대하여 참이라면 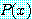 는 참이다.
는 참이다.
마찬가지로 존재 정량 명제는 개별의 명제
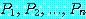 의 복합 명제
의 복합 명제
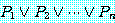 (7)
(7)
를 일반화한 것이고 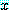 가 담화 영역의 일원일 때, 정해지지 않은
가 담화 영역의 일원일 때, 정해지지 않은 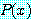 의 구성원을 재배치하여 만들었으며, 따라서 (7) 도
의 구성원을 재배치하여 만들었으며, 따라서 (7) 도
for some 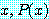
와 같이 쓸 수 있다.
지금까지 정리 12 가 어떻게 드모르간의 논리 법칙 (예제 1.2.11) 을 일반화했는지 설명하였다. 첫 번째 드모르간의 논리 법칙이 다음 명제들
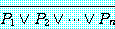 and
and 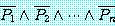
이 같은 진리값을 가지고 있다는 것을 이야기했음을 상기하자.
정리 12 의 part (b) 에서,
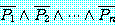
는
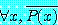
와 같이 다시 쓸 수 있고
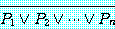
는
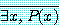
로 대신할 수 있다.
(예제 14)
문장들은 가끔 하나의 이상의 해석이 가능하다. 세익스피어의 유명한 말을 인용해 보자.
반짝인다고 모두 금은 아니다 (All that glitters is not gold.).
이 인용문의 한 가지 가능한 해석은 "반짝이지 않는 모든 것은 금이다 (즉, 금은 결코 반짝이지 않는다)." 이다. 그러나 이것은 세익스피어가 의도한 것이 확실히 아니다. 정확한 해석은 "반짝이는 것 중에는 금이 아닌 것이 있다." 인 것이다.
만약 명제 함수 "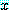 glitters" 를
glitters" 를 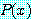 로 두고 명제 함수 "
로 두고 명제 함수 "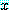 is gold" 를
is gold" 를 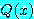 로 둔다면 첫 번째 해석은 이렇게 된다.
로 둔다면 첫 번째 해석은 이렇게 된다.
for all 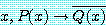 (8)
(8)
그리고 두 번째 해석은 이렇다.
for all 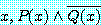
와
for all 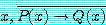
는 진리값이 같다는 사실을 알 수 있다. 정리 12 에 의해서
for some 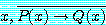
와
|
for all |
의 진리값이 같다. 그러므로 두 번째 해석은
|
for all |
(9) |
와 같게 표현된다.
8 과 9 를 비교해 보면 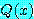 를 부정으로 적용했는지 (첫 번째 해석) 아니면 전체의 진술로 적용했는지 불확실한
결과임을 알 수 있다.
를 부정으로 적용했는지 (첫 번째 해석) 아니면 전체의 진술로 적용했는지 불확실한
결과임을 알 수 있다.
for all 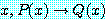
(두 번째 해석) 그 문장의 올바른 해석은
반짝인다고 모두 금은 아니다,
이며, 이는 전체 문장을 부정한 결과이다.
긍정문에서 "any" "all", "each", "every" 는 같은 의미를 가진다. 부정문은 상황이 바뀐다.
|
Not all Not each Not every |
는
Some 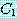 is not
is not 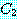
인데 반하여
Not any 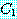 is
is 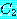
는
No 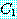 is
is 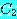
이다.
다른 예들로 연습 문제 47 과 48 을 준비했다.
다음 예에서는 한 문장 안에서 전체와 존재 정량자가 어떻게 섞여서 나타나는지 그리고 하나 이상의 변수가 사용되는 경우 어떻게 표현되는지를 보여 줄 것이다.
(예제 15)
실수의 집합이 담화 영역인 경우를 생각해 보자. 다음 문장
for every 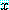 , for some
, for some 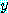 ,
, 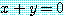
의 의미는 어떤 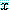 라 하더라도
라 하더라도 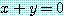 을 만족하는
을 만족하는 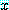 의 선택에 의존하는 최소 하나 이상의
의 선택에 의존하는 최소 하나 이상의 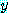 가 있다는 것이다. 문장
가 있다는 것이다. 문장
for every 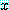 , for some
, for some 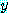 ,
, 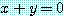
은 참이다. 어떤 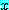 에 대해서도
에 대해서도 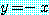 인 하나 이상의
인 하나 이상의 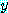 를 찾을 수 있다.
를 찾을 수 있다.
그러므로 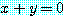 은 참이다.
은 참이다.
예제 15 의 문장을 수정하여 다음과 같이 적어보자.
for some 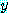 , for every
, for every 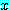 ,
, 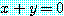
이 참이 되도록 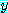 에 어떤 값을 고를 수 있다. 그러나 반례로 마지막 문장이 그릇됨을 증명할 수
있다. 예를 들어,
에 어떤 값을 고를 수 있다. 그러나 반례로 마지막 문장이 그릇됨을 증명할 수
있다. 예를 들어, 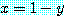 로 생각할지라도 우리는 잘못된 문장
로 생각할지라도 우리는 잘못된 문장
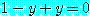
을 얻는다. 그러므로 위 문장
for some 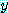 , for every
, for every 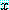 ,
, 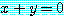
은 거짓이다.
(예제 16)
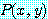 를
를
if 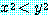 , then
, then 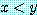
라는 문장이라 하자. 담화 영역은 실수의 집합이다.
이 문장은
for every 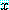 , for every
, for every 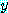 ,
, 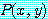
일 때 거짓이다. 반례는 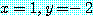 일 때이다. 이 경우
일 때이다. 이 경우
if 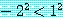 then
then 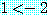
와 같은 잘못된 명제를 얻는다.
문장
for every 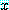 , for some
, for some 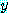 ,
, 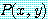
는 참이다. 모든 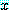 에 대하여 다음 명제
에 대하여 다음 명제
for some 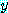 , if
, if 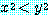 , then
, then 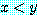
는
if 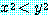 , then
, then 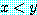
이 참이 되도록 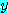 의 값을 나타내는 것에 의해 참이 된다. 사실, 만약
의 값을 나타내는 것에 의해 참이 된다. 사실, 만약 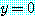 이면 참인 명제를 얻는다.
이면 참인 명제를 얻는다.
if 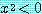 , then
, then 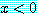
(가설 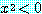 가 거짓이기 때문에 이 조건부 명제는 참이다.)
가 거짓이기 때문에 이 조건부 명제는 참이다.)
문장
for every 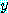 , for some
, for some 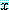 ,
, 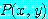
는 참이다. 명제
for some 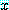 , if
, if 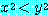 , then
, then 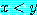
는
if 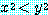 , then
, then 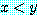
가 참인 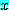 의 값을 고려했을 때, 참이 되므로 모든
의 값을 고려했을 때, 참이 되므로 모든 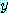 에 대해서 참이다. 사실,
에 대해서 참이다. 사실, 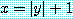 일 때 참인 명제
일 때 참인 명제
if 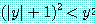 , then
, then 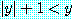
를 얻는다 (가정이 거짓이므로 조건부 명제는 참이다).
여기서 전체 혹은 존재 정량 문장을 증명하거나 반증하기 위한 규칙을 요약한다.
for every 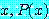
를 참으로 증명하기 위하여, 담화 영역의 모든
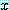 에 대하여
에 대하여 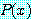 가 참임을 보이면 된다.
가 참임을 보이면 된다.
for every 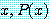
가 참이라고 증명되지 않은 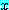 의 특별한 값에 대하여
의 특별한 값에 대하여 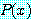 가 참임을 보인다.
가 참임을 보인다.
for some 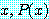
를 참으로 증명하기 위하여, 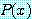 가 참이 되는 담화 영역 속에 한 값을 찾는다. 한 값으로 충분하다.
가 참이 되는 담화 영역 속에 한 값을 찾는다. 한 값으로 충분하다.
for every 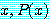
를 거짓으로 증명하기 위해서는 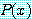 가 거짓이 되는 담화 영역 속에
가 거짓이 되는 담화 영역 속에 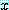 의 한 값 (반례) 을 찾는 것이다.
의 한 값 (반례) 을 찾는 것이다.
for some 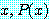
를 거짓으로 증명하기 위해서는 담화 영역
속에 모든 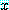 에 대하여 명제
에 대하여 명제 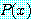 가 거짓임을 보여야 한다. 이를 위하여
가 거짓임을 보여야 한다. 이를 위하여
for some 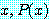
가 거짓이라고 증명되지 않은 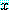 의 특별한 값에 대하여
의 특별한 값에 대하여 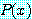 가 거짓임을 보인다.
가 거짓임을 보인다.