Tree 의 용어와 특성

이산수학 : Richard Johnsonbaugh 저서, 강홍식.김정인.이도훈.이명재 번역, 교보문고, 1999 (원서 : Discrete Mathematics 6th ed, Prentice-Hall, 1997), Page 459~464

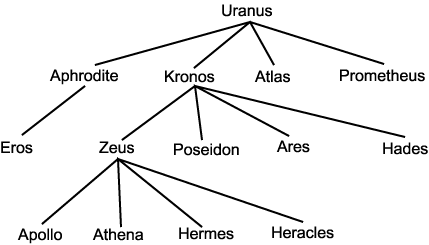
고대 그리이스 신들의 가계도의 일부분을 그림 1 에 나타내었다 (모든 자식들을 열거하지는 않았음). 보이는 것처럼 우리는 가계도를 뿌리 있는 트리로 간주할 수 있다. 정점 v 에 인접하고 바로 아래 레벨에 있는 정점들은 v 의 자식들이다. 예를 들어, 크로노스의 자식은 제우스, 포세이돈, 헤이디즈, 그리고 아레스이다. 가계도에서 채택한 용어가 모든 뿌리 있는 트리에서 그대로 사용된다. 공식적인 정의는 다음에 있다.

 (정의 1)

T를 뿌리 v₀를 가진 트리라고 하자. x, y 그리고 z 는 T 의 정점들이고, (v₀, v₁, …, v_n) 은 T 에서의 단순 경로라고 가정하자. 그러면

(a) v_n-1

은 v_n 의 부모 (parent) 이다.

(b) v₀, v₁, …, v_n - 1 은 v_n 의 조상 (ancestor) 이다.

(c) v_n 은 v_n - 1 의 자식 (child) 이다.

(d) 만약 x 가 y 의 조상이라면, y 는 x 의 후손 (descendent) 이다.

(e) x 와 y 가 z 의 자식이라면, x 와 y 는 형제 (sibling) 이다.

(f) x 가 자식을 갖지 않는다면, x 는 말단 정점 (internal vertex 즉, branch) 이다.

(g) x 가 말단 정점이 아니면, x 는 내부 정점 (internal vertex 즉, branch) 이다.

(h) x를 뿌리로 하는 T 의 부분 트리 (subtree) 는 다음과 같은 정점 집합 V 와 간선 집합 E 를 갖는 그래프이다. V 는 x 와 x 의 후손들이다.

그림 1  고대 그리이스 신들의 가계도의 일부분

E = { e|e 는 x에서 V 의 어떤 정점까지의 단순 경로상의 간선이다 }

 (예제 2)

그림 1 의 뿌리 있는 트리에서,

(a) 에로스의 부모는 아프로디테이다.

(b) 헤르메스의 조상은 제우스, 크로노스, 그리고 우라누스이다.

(c) 제우스의 자식은 아폴로, 아테나, 헤르메스, 그리고 헤라클레스이다.

(d) 크로노스의 후손은 제우스, 포세이돈, 헤이디즈, 아레스, 아폴로, 아테나, 헤르메스, 그리고 헤라클레스이다.

(e) 아프로디테와 프로메티우스는 형제이다.

(f) 말단 정점은 에로스, 아폴로, 아테나, 헤르메스, 헤라클레스, 포세이돈, 헤이디스, 아레스, 아틀라스, 그리고  프로메테우스이다.

(g) 내부 정점은 우라누스, 아프로디테, 크로노스, 그리고 제우스이다.

(h) 크로노스를 뿌리로 하는 부분 트리는 그림 2 와 같다.

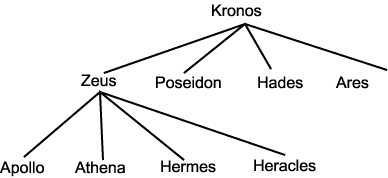
그림 2  그림 1 의 트리에서 크로노스를 뿌리로 하는 부분 트리

이 절의 나머지에서는 트리의 다른 특성을 살펴보도록 한다. T를 트리라 하자. 트리에서는 임의의 정점에서 다른 모든 정점으로의 단순 경로가 있으므로, T 가 연결되어 있다는 것을 알 수 있다. 게다가 T 는 순환 (cycle)을 포함하지 않는다는 것을 보일 수 있다. 이것을 보이기 위해서, T 가 순환 C' 를 포함한다고 가정하자. 정리 6.2.24 에 의해서 T 는 v₀ = v_n 인 단순 순환

C = (v₀, …, v_n)

을 포함한다 (그림 3). T 는 단순 그래프이므로 C 는 루프가 될 수 없다 ; 그러므로 C 는 적어도 i < j 인 두 개의 구별되는 정점 v_i 와 v_j 를 포함한다. 이제

(v_i, v_i+1, ..., v_j), (v_i, v_i-1, ..., v₀, v_n-1, ..., v_j)

는 v_i 에서 v_j 로의 서로 다른 단순 경로들이다. 이것은 트리의 정의에 모순이 된다. 그러므로 트리는 순환을 포함할 수 없다.

순환을 갖고 있지 않는 그래프를 비순환 그래프 (acyclic graph) 라고 부른다. 우리는 방금 트리는 연결되어 있고, 비순환 그래프라는 것을 보였다. 역도 역시 성립한다 ; 연결되어 있고 비순환인 모든 그래프는 트리이다. 다음 정리는 트리의 이런 특성과 함께 다른 특성들도 제시한다.

그림 3  단순 순환

 (정리 3)

T 를 n 개의 정점을 가진 그래프라고 하자. 다음은 모두 동등하다.

(a) T 는 트리이다.

(b) T 는 연결되어 있고 비순환이다.

(c) T 는 연결되어 있고 n-1 개의 간선을 갖는다.

(d) T 는 비순환이고 n-1 개의 간선을 갖는다.

 증명   (a) 부터 (d) 까지가 동등하다는 것을 보이기 위해, 다음의 4 가지 결과를 증명할 것이다. :

(a) 이면 (b) ; (b) 이면 (c) ; (c) 이면 (d) ; 그리고 (d) 이면 (a). [(a) 이면 (b)] 이것에 대한 증명은 이 정리 앞에서 이미 제시하였다.

[(b) 이면 (c)] T 가 연결되어 있고 비순환이라고 가정한다. T 가 n-1 개의 간선을 갖는다는 것을 n 에 대한 귀납법으로 증명할 것이다.

만약 n=1 이면, T 는 간선은 없고 단지 하나의 정점으로 구성된다. 그러므로 n=1 인 경우에 성립한다.

이제는 이 결과가 n 개의 정점을 갖고 있는 연결되어 있고 비순환 그래프에서 성립한다고 가정하자. T 를 n+1 개의 정점을 갖는 연결되어 있고 비순환 그래프라고 하자. T 를 n+1 개의 정점을 갖는 연결되어 있고 비순환 그래프라고 하자. 최대 길이의 단순 경로 P 를 선택한다. T 가 비순환이므로, P 는 순환이 아니다. 그러므로 P 는 차수가 1 인 정점 v 를 포함한다 (그림 4). T^* 를 T 에서 정점 v 와 v 에 부속된 간선을 제거한 것이라고 하자. 그러면, T^* 는 연결되어 있고 비순환이다. 또한 T^* 는 n 개의 정점을 가지므로 가정에 의해 T^* 는 n-1 개의 간선을 갖는다. 그러므로 T 는 n 개의 간선을 갖는다.

따라서 수학적 귀납법에 의해 이 결과는 성립한다. [(c) 이면 (d)] T 가 연결되어 있고 n-1 개의 간선을 갖는다고 가정하자. 우리는 T 가 비순환이라는 것을 보여야 한다.

T 가 적어도 하나의 순환을 갖는다고 가정하자. 순환에서 하나의 간선을 제거하더라도 그래프는 계속 연결되어 있으므로, 결과 그래프인 T^* 가 연결되어 있고 비순환이 될 때까지 T 에서 순환을 구성하는 간선들을 (정점들은 제거하지 않고) 제거할 수 있다. 이제 T^* 는 n 개의 정점을 가진 연결되어 있고 비순환 그래프이다. 우리는 T^* 가 n-1 개의 간선을 갖는다고 결론 짓기 위해 앞에서 증명한 (b) 이면 (c) 라는 결과를 사용할 수 있다. 그러나 이제는 T 가 n-1 개 보다 많은 수의 간선들을 갖는다. 이것은 모순이다. 그러므로 T 는 비순환이다. 이 결과에 대한 증명이 완성된다. [(d) 이면 (a)] T 가 비순환이고 n-1 개의 간선을 갖는다고 가정하자. 우리는 T 가 트리 즉, T 가 단순 그래프이고, T 는 임의의 정점에서 다른 정점으로의 유일한 단순 경로를 갖는다, 는 것을 보여야 한다. 루프는 순환이고 T 는 비순환이라고 했으므로, 그래프 T 는 어떠한 루프도 포함할 수 없다. 마찬가지로 T 는 v 와 w 에 부속된 서로 다른 간선 e₁ 과 e₂ 를 포함할 수 없다. 왜냐하면 만약 그렇게 된다면 순환 (v, e₁, w, e₂, v) 를 가지게 되기 때문이다. 그러므로 T 는 단순 그래프이다.

모순에 의한 증명을 하기 위해, T 가 연결되어 있지 않다고 가정하자 (그림 5). 그리고

T₁, T₂, …, T_k

를 T 의 요소들이라고 하자. T 가 연결되어 있지 않으므로, k > 1 이다. T_i 가 n_i 개의 정점을 갖는다고 가정하자. 각각의 T_i 는 연결되어 있고 비순환이므로, 앞에서 증명한 결과인 (b) 이면 (c) 에 의해 T_i 는 n_i-1 개의 간선을 갖는다. 그러면,

n - 1   =   (n₁ - 1) + (n₂ - 1) + … + (n_k - 1)            (간선들의 수를 더함)

                <   (n₁ + n₂ + …  + n_k) - 1                          (k > 1 이므로)

                =    n - 1                                                 (정점의 수)

라는 모순된 식이 발생하게 된다. 그러므로 T 는 연결되어 있다.

T 에서, a 에서 b 로의 서로 다른 단순 경로 P₁ 과 P₂ 가 존재한다고 가정하자 (그림 6). c 를 a 다음에 있으면서 P₁ 상에 는 있고 P₂ 상에는 없는 첫 번째 정점이라고 하자 ; d 를 P₁ 상에서 c 바로 앞의 정점이라고 하자 ; 그리고 e 를 d 다음에 있으면서, P₁ 과 P₂ 상에 모두 있는 첫 번째 정점이라고 하자.

(v₀, v₁, …, v_n-1, v_n)

을 d = v₀ 에서 e = v_n 까지인 P₁ 의 일부분이라고 하자. 그리고

(w₀, w₁, …, w_m-1, w_m)

을 d = w₀ 에서 e = w_m 까지인 P₂ 의 일부분이라고 하자. 그러면,

(v₀, …, v_n = w_m, w_m-1, …, w₁, w₀)                  (1)

은 T 에서의 순환이 되고, 모순이 발생하게 된다. [(1) 은 v₀ 와 w₀ 를 제외하고는 반복되는 정점이 없으므로 단순 순환이다.] 따라서 T 는 임의의 정점에서 다른 정점으로의 유일한 단순 경로를 갖는다. 그러므로 T 는 트리이다.