Spanning Tree
이산수학 : Richard Johnsonbaugh 저서, 강홍식.김정인.이도훈.이명재 번역, 교보문고, 1999 (원서 : Discrete Mathematics 6th ed, Prentice-Hall, 1997), Page 469~475
이 절에서는, 그래프 G 의 모든 정점들을 포함하는 트리인 부분 그래프 T 를 찾는 문제를 고려해 본다. 이런 트리를 신장 트리 (spanning tree) 라고 부른다. 신장 트리를 찾는 방법이 다른 문제들에도 잘 적용될 수 있다는 것을 보일 것이다.
그림 1 그래프와 진한 점선으로 표시한 신장트리
(정의 1)
T 가 그래프 G 의 모든 정점을 포함하는 부분 그래프로서 트리이면, T 는 G 의 신장 트리 (spanning tree) 이다.
그림 2 그림 1의 그래프 G 의 다른 신장 트리 (진한 점선으로 표시)
(예제 2)
그림 1 의 그래프 G 의 신장 트리는 점선으로 표시한 것이다
(예제 3)
일반적으로 하나의 그래프는 여러 개의 신장 트리를 갖는다. 그림 1 의 그래프 G 의 다른 신장 트리를 그림 2 에 나타내었다.
그래프 G 가 신장 트리 T 를 갖고 있다고 가정한다. 그리고 a 와 b 를 T 의 정점들이라고 하자. 그러면, a 와 b 는 T 의 정점들이고 T 는 트리이므로, a 에서 b 로의 경로 P 가 존재한다. 그러나 P 는 G 에서도 또한 a 에서 b 로의 경로의 역할을 한다 ; 따라서 G 는 연결되어 있다. 이것의 역도 또한 성립한다.
(정리 4)
"그래프 G 가 신장 트리 T 를 갖는다." 는 "G 가 연결되어 있다." 의 필요 충분 조건이다.
증명 우리는 이미 G 가 신장 트리를 가지면, G 가 연결되어 있다는 것을 보였다. G 가 연결되어 있다고 가정하자. 만약 G 가 비순환적이면, 정리 3 에 의해 G 는 트리이다.
G 가 순환을 포함한다고 가정하자. 이 순환에서 간선 하나 (정점은 그대로 둠) 를 제거한다. 생선된 그래프는 아직도 연결되어 있다. 만약 그것이 비순환적이면, 작업을 멈춘다. 만약 순환을 포함한다면, 이 순환에서 간선 하나를 제거한다. 이런 식으로 계속하면, 궁극적으로 비순환적이고 연결되어 있는 부분 그래프 T 를 생성할 수 있다. 정리 3 에 의해 T 는 트리이다. 또한 T 가 G 의 모든 정점들을 포함하므로, T 는 G 의 신장 트리이다.
정리 4 의 증명을 기초로 한 신장 트리를 찾는 알고리즘은 매우 효율적이지는 않을 것이다 ; 순환을 찾는 데 많은 시간을 소요할 것이다. 우리는 좀더 나은 방법으로 이 작업을 수행할 수 있다. 먼저 신장 트리를 찾는 알고리즘을 예를 통해 설명하고, 그 다음 알고리즘을 기술하겠다.
(예제 5)
그림 1의 그래프 G 에 대한 신장 트리를 구하여라.
너비 우선 검색 (Breadth First Search) 이라는 방법을 사용할 것이다 (알고리즘 6). 너비 우선 검색의 기본 생각은 다음의 높은 레벨로 이동하기 전에 주어진 레벨에 있는 모든 정점들을 방문하는 것이다. 먼저 G 의 정점들의 순서, 예를 들어 abcdefgh 를 정한다. 그리고 첫 번째 정점 a 를 선택하고, 그것을 뿌리로 한다. T 를 간선은 없고 하나의 정점 a 로 구성된 것이라고 하자. 그리고 x = b 부터 h 에 대해, a 에 인접한 정점 x 와 간선 (a, x) 가 T 에 추가되었을 때 순환을 생성하지 않으면 이들을 T 에 추가한다. T 에 간선 (a, b), (a, c) 그리고 (a, g) 가 추가될 것이다 (a 와 g 에 부속된 parallel 간선들 중 어떤 것도 사용할 수 있다). 레벨 1인 정점들에 대해서도 각각을 순서대로 검사하면서 이 작업을 반복한다 ;
b : (b, d) 를 포함.
c : (c, e) 를 포함.
g : 포함할 것이 없음.
레벨이 2 인 정점들에 대해서도 이 작업을 반복한다 :
d : (d, f) 를 포함.
e : 포함할 것이 없음.
레벨이 3 인 정점들에 대해서도 이 작업을 반복한다.
f : (f, h) 를 포함.
레벨이 4 인 정점 h 에서는 어떠한 간선도 추가될 수 없으므로, 이 작업은 끝이 난다. 우리는 그림 1 에 나타낸 것과 같은 신장 트리를 구하였다.
예제 5의 방법을 정형화한 것이 알고리즘 6이다.
(알고리즘 6)
신장 트리를 구하기 위한 너비 우선 검색이 알고리즘은 너비 우선 검색 방법을 사용하여 신장 트리를 찾아낸다.
입력: v1, v2, ..., vn 으로 순서화된 정점들을 갖는 연결 그래프 G
출력: 신장 트리 T
procedure bfs (V, E)
// V = v1, v2, ..., vn 으로 순서화된 점점들 ; E = 간선들
// V' = 신장 트리 T 의 정점들 ; E' = 신장 트리 T 의 간선들
// v1 은 신장 트리의 뿌리
// S 는 순서화된 목록
S : = {v1}
V' : = {v1}
E' : = Ø
while true do
begin
for 각각의 x ∈ S, 순서대로 do
for 각각의 y ∈ V - V', 순서대로 do
if (x, y) 가 간선 then
간선 (x, y) 를 E' 에, 그리고 y 를 V' 에 추가
if 추가된 간선이 없음 then
return (T)
S : = 원래의 정점들의 순서와 일치하는 순서로 S 의 자식들
end
end bfs
연습 문제 16 은 알고리즘 6 이 신장 트리를 정확하게 찾는다는 것을 증명하는 것이다. 너비 우선 검색은 n 개의 정점을 가진 임의의 그래프 G 가 연결되어 있는지 아닌지를 검사하는 데도 사용될 수 있다 (연습 문제 26). 우리는 트리 T 를 생성하기 위해 알고리즘 6 의 방법을 사용한다. 그러면 "G 가 연결되어 있다." 는 "T 가 n 개의 정점을 갖는다." 의 필요 충분 조건이다.
너비 우선 검색은 또한 가중치가 없는 그래프에서 고정된 정점 v 에서 모든 다른 정점들의 최소 길이 경로를 찾는 데도 사용될 수 있다 (연습 문제 20). 우리는 알고리즘 6 의 방법을 v 를 뿌리로 하는 신장 트리를 생성하기 위해 사용한다. 우리는 신장 트리에서 정점 v 에서 레벨 i 인 정점으로의 최소 경로의 길이는 i 라는 것을 알 수 있다. Dijkstra 의 가중 그래프에 대한 최소 경로 알고리즘 (알고리즘 6.4.1) 은 너비 우선 검색을 일반화한 것으로서 간주될 수 있을 것이다 (연습 문제 21).
너비 우선 검색의 대안은 깊이 우선 검색 (Depth First Search) 이다.
(알고리즘 7) 신장 트리를 구하기 위한 깊이 우선 검색
이 알고리즘은 깊이 우선 검색 방법을 사용하여 신장 트리를 찾아낸다.
입력 : v1, v2, ..., vn 으로 순서화된 정점들을 갖는 연결 그래프 G
출력: 신장 트리 T
procedure bfs (V, E)
//
V' = 신장 트리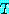 
의 정점들 ; E' = 신장 트리 T 의 간선들
// v1 은 신장 트리의 뿌리
V : = {v1}
E' : = Ø
w : = v1
while true do
begin
while 간선이 T 에 추가되었을 때 순환을 생성하지 않는 간선 (w, v) 가 있으면 do
begin
간선이 T 에 추가되었을 때 순환을 생성하지 않는 최소 레벨의
간선(w, vk) 를 선택한다.
vk 를 V' 에 추가한다.
w : = vk
end
if w = v1 then
returm (T)
w : = T 에 있는 w 의 부모 // 되돌아감
end
end dfs
연습 문제 17은 알고리즘 7 이 신장 트리를 정확하게 찾는다는 것을 증명하는 것이다.
(예제 8)
정점들의 순서를 abcdefgh 로 해서 그림 2 의 그래프에 대한 신장 트리를 구하기 위해, 깊이 우선 검색 (알고리즘 7) 을 사용하여라. 먼저 첫 번째 정점 a 를 선택하고, 그것을 뿌리로 한다 (그림 2). 그 다음 최소 레벨을 갖는 x 에 대해, 간선 (a, x) 를 트리에 추가한다. 여기서는 간선 (a, b) 가 추가된다.
이 작업을 반복하여, 간선 (b, d), (d, c), (c, e), (e, f) 그리고 (f, h)를 추가한다. 이 시점에서 우리는 (h, x) 형식의 간선을 추가할 수 없다. 따라서 h 의 부모 f 로 되돌아가서 (f, x) 형식의 간선을 추가하려고 시도한다. 그러나 여기서도 역시 (f, x) 형식의 간선을 추가할 수 없으므로, f 의 부모 e 로 되돌아간다. 이번에는 간선 (e, g) 를 성공적으로 추가할 수 있다. 이제는 더 이상의 간선들을 추가할 수 없으므로, 마침내 뿌리로 되돌아가게 되고, 작업은 끝이 난다.
알고리즘 7 중에서, 처음에 선택된 뿌리를 향해 간선을 따라 되돌아가는 라인 때문에, 깊이 우선 검색을 백트래킹 (backtracking) 이라고도 부른다. 다음 예제에서는 문제를 풀기 위해 백트래킹을 사용한다.
(예제 9) 4-퀸 문제
4-퀸 문제는 4 × 4 그리드 상에 어떠한 두 토큰도 동일한 행, 열, 혹은 대각선에 놓이지 않도록 4 개의 토큰을 위치시키는 문제이다. 4-퀸 문제를 해결하기 위한 백트래킹 알고리즘을 구성하여라 (이런 용어를 사용한 이유는, 이것이 4 × 4 체스판에서 어떠한 퀸도 다른 퀸을 공격할 수 없도록 4 개의 퀸을 배치하는 문제이기 때문이다.)
알고리즘의 기본 생각은 열에 토큰을 계속적으로 위치시키는 것이다. 어떤 열에 토큰을 배치하는 것이 불가능할 때는, 되돌아가서 앞의 열의 토큰의 위치를 조정한다.
(알고리즘 10) 백트래킹을 사용한 4-퀸 문제의 해결 방법
이 알고리즘은 4 × 4 그리드 상에 어떠한 두 토큰도 동일한 행, 열, 혹은 대각선에 놓이지 않도록 4 개의 토큰을 배치하는 방법을 찾기 위해 백트래킹을 사용한다.
입력: 크기 4 인 행의 배열
출력: true, 해결책이 있으면
false,
해결책이 없으면[만약 해결책이 있으면,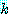 
번째 퀸은 열 
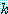, 행 
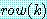에 놓인다.]
procedure four_queens (row)
k : = 1 // 1 열에서 시작
// row (k) 는 사용되기 전에 증가된다, 따라서 1 행에서 시작한다.
row (1) : = 0
while k, > 0 do
begin
row(k) : = row(k) + 1
// k 열에서의 합법적인 이동점을 찾는다.
while
row(k)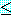 
4 and k 열, row(k) 가 충돌하면, do
// 다음 행에서 시도한다.
row(k) : = row(k) + 1
if
row(k)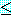 
4 then //
k 열에서 합법적인 이동점을 찾음.
if k = 4 then // 해결책 완성
return(true)
else // 다음 열
begin
k : = k + 1
row(k) : = 0
end
else // 이전 열로 되돌아감
k : = k - 1
end
returm(false) // 해결책 없음
end four_queens
알고리즘 10 이 생산하는 트리를 그림 3 에 나타내었다. 번호는 정점들이 생성된 순서를 나타낸다. 해결책은 정점 8 에서 구해졌다. n-퀸 문제는 n × n 그리드 상에 어떠한 두 토큰도 동일한 행, 열, 혹은 대각선에 놓이지 않도록 n 개의 토큰을 위치시키는 문제이다. 2-퀸 또는 3-퀸 문제에는 해결책이 없다는 것을 보이는 것은 어렵지 않다 (연습 문제 10). 우리는 방금 알고리즘 10 이 4-퀸 문제에 대한 해결책을 생성하는 많은 방법이 제안되었다 (참고 문헌 [Erbas] 등을 보아라).
백트래킹 즉, 깊이 우선 검색은 원하는 것이 하나의 해결책인 예제 9 와 같은 문제에서는 특별히 매력적이다. 만약 해결책이 존재한다면, 해결책은 말단 정점에서 구해지므로, 가능한 빨리 말단 정점으로 이동하는 것에 의해서 불필요한 정점들을 생성하는 것을 피할 수 있다.
그림 3 4-퀸 문제에 대한 해결책을 위한 검색에서 백트래킹 알고리즘(알고리즘 10) 이 생성하는 트리