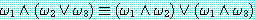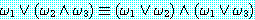 (BAT_OK)
(BAT_OK)
 (LIFTABLE)
(LIFTABLE)
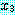 (MOVES)
(MOVES)
명제논리
(Propositional Calculus)
인공지능-지능형 에이전트를 중심으로 : Nils J.Nilsson 저서, 최중민. 김준태. 심광섭. 장병탁 공역, 사이텍미디어, 2000 (원서 : Artificial Intelligence : A New Synthesis 1998), Page 229~242
우리는 앞에서 에이전트 세계를 모델링하는 두 가지 서로 다른 방법으로 아이콘 (icon) 을 기반으로 한 것과 특징 (feature) 을 기반으로 한 것에 대해 살펴보았다. 이진값을 갖는 특징들은 모델링하는 세계에서 무엇이 사실이고 무엇이 사실이 아닌지에 대한 묘사 (description) 이다. 아이콘기반 표현 방식은 그 세계의 특정 측면에 대한 시뮬레이션 (simulation) 이다. 대개의 경우, 시뮬레이션이 묘사보다 직접적이고 효과적이긴 하지만 묘사도 나름대로의 장점이 있다. 에이전트 사이의 통신의 경우, 특징값들은 다른 에이전트에게 전달되기 쉬운 반면, 아이콘 모델은 독립적인 조각들로 나누어 점진적인 (incremental) 통신을 하기가 어렵다. 또한 특징값을 계산하는 데에 필요한 인지 과정은 아이콘 모델을 만들거나 수정하는 것보다 훨씬 간단하다. 그리고 어떤 특성들의 값을 직접 인식하기 어려운 경우, 에이전트가 속한 세계에 있는 제약조건들을 이용하여 다른 특징값들로부터 그 값을 추론할 수도 있다.
뿐만 아니라, 에이전트 환경의 어떤 정보에 대해서는 아이콘화하여 표현하기가 어렵거나 불가능한 경우가 있다. 다음의 예를 보자.
이와 같이 표현하기 어려운 정보의 일부는 특징값에 대한 제약조건 (constraints) 으로 공식화될 수 있다. 에이전트가 존재하는 세계에 대한 중요한 지식을 표현하는 제약조건들은 직접 인식될 수 없는 특징값들을 추론하는데 많이 이용된다 (특징들 사이의 제약조건에 기반을 둔 계산을 수행하여). 에이전트의 현재 상태에 대한 정보를 추측하는 것은 (이 책의 2 부에 설명한 탐색 방법들을 이용하여) 에이전트의 행동의 결과로 나타나는 미래 상태를 계산하는 것과 대조된다. 처음 행위를 추론 (reasoning), 나중 것을 투영 (projecting) 이라고 하며, 다음 몇 개 장에서는 투영 문제는 접어 두고 추론에 대해 집중적으로 다룰 것이다.
특징값을 추론하는 것과 관련된 몇 가지 응용 분야가 있다. 무엇보다 추론은 에이전트가 행동을 결정할 때 에이전트의 효율성을 높여 준다 (반응형 에이전트인 경우에도). 다른 응용 분야도 많이 있는데 예를 들어, 생물이나 전자 기계 시스템 등의 물리적인 시스템의 기능을 적절한 특징의 집합으로 표시할 수 있다는 것이 알려져 있으며, 이 특징들 사이의 제약조건들은 조직이나 장치에 관한 물리적 혹은 그 밖의 규칙을 나타낸다. 이런 경우 추론은 시스템의 장애를 진단하는 등의 목적으로 사용될 수 있다. 예를 들어, "원인" 과 관련된 특징들을 "증상" 과 관련된 특징들로부터 추론할 수 있다. 이와 같은 일반적인 접근 방식은 AI 의 중요한 응용 분야의 하나인 전문가 시스템에 매우 중요하다.
추론 방법들을 설명하기에 앞서 동기를 부여할 만한 예제를 하나 살펴보자. 블록이 너무 무겁지 않고, 로봇의 배터리 파워 소스가 적절하면 블록을 들 수 있는 로봇을 생각해 보자. 만일 이 두 가지 조건이 만족된다면 로봇이 자신이 잡고 있는 블록을 들려고 할 때 팔이 움직일 것이다. 우리는 이 여러 가지 조건들을 이진값을 갖는 특징들로 다음과 같이 표현할 수 있다.
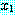 (BAT_OK)
(BAT_OK)
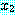 (LIFTABLE)
(LIFTABLE)
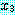 (MOVES)
(MOVES)
설명을 돕기 위해 괄호 안의 특징을 기억하기 쉬운 이름들로 지었다. 로봇이 계기를 읽어 BAT_OK 를, 조인트 각도 센서를 이용하여 MOVES 를 감지할 수 있고 LIFTABLE 은 알 수 없다고 가정하자. 그러나 LIFTABLE 의 값은 로봇이 수행해야 하는 일을 결정하는 데 매우 중요하다. 우리의 예제에서는 BAT_OK 와 LIFTABLE 의 값이 1 일 때 MOVES 도 1 이다. 만일 로봇이 움직이려 시도했을 때, MOVES 가 0 이라면 BAT_OK 이나 LIFTABLE 의 값 중 하나는 0 이어야 한다. BAT_OK 값이 1 로 감지되었다면 LIFTABLE 의 값이 0 이어야 한다. 우리가 이와 같이 추론할 수 있으므로, 로봇도 이렇게 할 수 있도록 해보자. 이를 위해 특징 사이의 제약조건과 특징값을 표현할 수 있는 언어 (language) 와 필요한 추론을 수행할 수 있는 추론 방법 (inference mechanism) 이 필요하다. 부울 대수에서 파생된 명제논리 (propositional calculus) 가 이러한 필요한 도구들을 제공한다.
위 예제의 제약조건은 명제논리 언어로 다음과 같이 나타낼 수 있다.
BAT_OK ∧ LIFTABLE ⊃ MOVES
여기서 ∧ 는 그리고 (and) 를, ⊃ 는 함의하다 (implies) 를 의미한다.
이 언어에는 주어진 문장으로부터 결론을 유도하는 데 이용할 수 있는 기법들이 있다. 인공지능에서는 논리언어들이 매우 중요하므로 이 언어들을 기반으로 하는 더 복잡하고 지능적인 에이전트를 소개하기 전에 이 기법들에 대해 자세히 다룰 것이다.
우선 몇 가지 정의가 있다. 논리 (logic) 는 다음을 포함한다.
여기서는 두 가지 논리언어에 대하여 소개할 것이다. 첫 번째는 두 가지 중 상대적으로 간단한 명제논리 (propositional calculus) 이고, 두 번째는 더 유용하게 이용되는 일차 술어논리 (first-order predicate calculus, FOPC) 이다. 일차 술어논리에서의 중요한 많은 개념들이 명제논리에서 보다 간단하게 설명될 수 있으므로 명제논리를 우선 소개하겠다.
명제논리의 요소들을 체계적으로 설명하겠다. 우선은 이 언어의 요소들을 의미와 결부시키지 않는 것이 좋다. 지금부터 우리가 하는 일을 의미 없는 게임의 규칙을 설명하는 것으로 생각하자. 의미에 대해서는 나중에 이야기할 것이다. 이 언어의 요소들은 다음과 같다.
아톰 (atoms) : 두 아톰 T 와 F 그리고 P, Q, R, ..., P1, P2, ON_A_B 등과 같이 대문자로 시작하는 문자열의 무한 대 집합.
연결자 (connectives) : "또는 (or)", "그리고 (and)", "함의 (implies)", "부정 (not)" 을 각각 나타내는 ∨, ∧, ⊃, ¬ (나중에 이 연결자들의 의미를 이름과 관련해 설명하겠다. 지금은 그냥 의미가 없는 기호들이라고 하자).
문장 (sentences) 이라고도 하는 정형식 (well-formed formulas, wffs) 의 문법 :
아톰들은 wff 이다.
ㆍ예 : P, R, P3
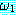 과
과 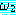 가 wff 이면 다음도 wff 이다.
가 wff 이면 다음도 wff 이다.
ㆍ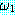 ∨
∨ 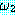 (
(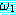 과
과 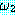 의 논리합 (disjunction))
의 논리합 (disjunction))
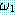 ∧
∧ 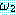 (
(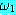 과
과 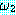 의 논리곱 (conjunction))
의 논리곱 (conjunction))
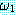 ⊃
⊃ 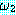 (함의 (implication))
(함의 (implication))
¬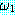 (
(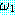 의 부정 (negation))
의 부정 (negation))
아톰과 ¬ 가 붙어 있는 아톰들을 리터럴 (literal)
이라고 한다. 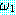 ⊃
⊃ 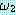 에서
에서 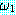 은 함의의 전제 (antecedent) 라고 하고
은 함의의 전제 (antecedent) 라고 하고 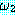 는 결론 (consequent) 이라고 한다.
는 결론 (consequent) 이라고 한다.
wff 의 예 :
(P ∧ Q) ⊃ ¬P
P ⊃ ¬P
P ∨ P ⊃ P
(P ⊃ Q) ⊃ (¬Q ⊃ ¬P)
¬¬P
ㆍ그 이외의 wff 는 없다.
예 : P ⊃ ¬¬는 wff 가 아니다.
앞의 예제에서 이용된 구별자 '(' 와 ')' 는 wff 들을 묶어 다시 wff 를 만드는 역할을 한다. 논리를 다룰 때 구별자를 언어의 일부로 공식화하여 다루는 경우도 있으나, 여기서는 그렇게까지 엄격하게 정의하여 사용하지는 않겠다. 어떤 문장이 wff 인지는 wff 의 정의를 재귀적으로 적용하여 판단할 수 있다. 예를 들어, (P ∧ Q) ⊃ ¬R 이 wff 임을 보이자. 우선, P 와 Q 가 wff 이므로 (P ∧ Q) 도 wff 이다. 또한 R 이 wff 이므로 ¬R 도 wff 이다. 그러므로 (P ∧ Q) ⊃ ¬R 은 wff 이다.
wff 들로부터 다른 wff 들을 만드는 방법은 여러
가지가 있는데, 이들을 추론 규칙 (rules of inference) 이라고 한다. 추론 규칙은
보통 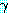 는 α 로부터 (혹은 α 와 β 로부터) 추론될 수 있다는 식의 형태를 가지고
있다. 다음은 흔히 이용되는 추론 규칙들이다.
는 α 로부터 (혹은 α 와 β 로부터) 추론될 수 있다는 식의 형태를 가지고
있다. 다음은 흔히 이용되는 추론 규칙들이다.
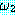 는 wff
는 wff 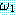 과 wff
과 wff 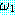 ⊃
⊃ 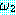 로부터 추론할 수 있다 (이 규칙을 모더스 포넌스 (modus ponens) 라고 한다).
로부터 추론할 수 있다 (이 규칙을 모더스 포넌스 (modus ponens) 라고 한다).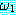 ∧
∧ 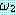 는 wff
는 wff 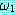 과
과 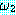 로부터 추론할 수 있다 (∧ 소개 (introduction))
로부터 추론할 수 있다 (∧ 소개 (introduction))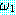 ∧
∧ 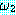 은 wff
은 wff 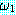 ∧
∧ 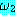 로부터 추론할 수 있다 (∧ 교환성 (commutativity)).
로부터 추론할 수 있다 (∧ 교환성 (commutativity)).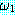 은 wff
은 wff 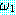 ∧
∧ 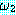 로부터 추론할 수 있다 (∧ 제거 (elimination)).
로부터 추론할 수 있다 (∧ 제거 (elimination)).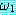 ∨
∨ 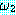 는 wff
는 wff 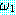 나 wff
나 wff 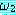 로부터 추론할 수 있다 (∨ 소개 (introduction)).
로부터 추론할 수 있다 (∨ 소개 (introduction)).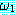 은 wff ¬(¬
은 wff ¬(¬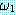 ) 로부터 추론할 수 있다 (¬ 제거 (elimination)).
) 로부터 추론할 수 있다 (¬ 제거 (elimination)).wff 의 순차 집합 (sequence) 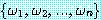 을 wff 의 집합 Δ 로부터의
을 wff 의 집합 Δ 로부터의 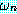 의 증명 (proof) (혹은 연역 (deduction)) 이라고 하는 것은, 순차 집합에 있는
각
의 증명 (proof) (혹은 연역 (deduction)) 이라고 하는 것은, 순차 집합에 있는
각 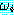 가 Δ 에 존재하거나 또는 순차 집합에서
가 Δ 에 존재하거나 또는 순차 집합에서 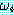 보다 앞에 나오는 wff 들로부터
보다 앞에 나오는 wff 들로부터 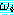 가 추론 규칙을 이용하여 추론될 수 있다는 것을 의미한다. Δ 로부터
가 추론 규칙을 이용하여 추론될 수 있다는 것을 의미한다. Δ 로부터 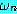 이 증명될 수 있다는 것을 다음과 같이 표기한다.
이 증명될 수 있다는 것을 다음과 같이 표기한다.
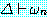
증명과 정리의 개념은 사용되는 추론 규칙의 집합과
관련이 있다. 추론 규칙의 집합을 문자 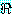 로 표기하면,
로 표기하면, 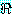 에 있는 추론 규칙을 이용하여 Δ 로부터
에 있는 추론 규칙을 이용하여 Δ 로부터 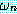 이 증명될 수 있다는 것을 다음과 같이 표기한다.
이 증명될 수 있다는 것을 다음과 같이 표기한다.
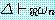
예 : wff 의 집합 {P, R, P ⊃ Q} 가 주어졌을 때, 다음의 순차 집합은 앞에 소개된 추론 규칙들에 의해 Q ∧ R 의 증명이 된다.
{P, P ⊃ Q, Q, R, Q ∧ R}
증명의 개념은 순차 집합뿐 아니라 부분 순서 (partial order) 로도 설명할 수 있다. 부분 순서는 트리 구조로 표시될 수 있다. 증명트리 (proof tree) 의 각 노드는 wff 가 되며, 반드시 Δ 에 있는 wff 이거나 트리의 부모 노드들로부터 추론 규칙을 이용하여 추론될 수 있는 것이어야 한다. 이 트리가 루트 노드에 대한 증명이다. 그림 1 에 증명트리의 예가 있다.
이제 의미 (meanings) 에 대해 논의해 보자. 의미론 (semantics) 은 논리언어의 요소들을 표현하고자 하는 문제 영역의 요소와 연관시키는 것이다. 이 연관이 바로 우리가 말하는 의미 (meanings) 이다. 명제논리의 경우, 아톰을 실세계에 대한 명제 (proposition) 에 연관시킨다 (그래서 이름이 명제논리이다). 예를 들어 아톰 BAT_OK 를 배터리가 충전되었다라는 명제에 연관시킬 수 있다 (아톰의 이름이 반드시 기억하기 쉬운 문자열일 필요는 없다. 이름을 다르게 지을 수도 있다). 아톰을 명제에 연관시키는 것을 해석 (interpretation) 이라고 한다. 주어진 해석에서 아톰과 연관된 명제를 그 아톰의 의미 (denotation) 라고 한다.
주어진 해석하에서 아톰은 그 값으로 True 혹은 False 를 갖는다. 만일 아톰 α 가 명제 P 와 연관되었다면 α 는 P 가 실세계에 대해 진실인 경우에 True 값을 가지며, 그렇지 않은 경우에는 False 값을 갖는다. 아톰 T 는 항상 True, 아톰 F 는 항상 False 값을 갖는 특별한 아톰이다. 실세계에 대한 명제들은 이상적으로는 항상 진실 아니면 거짓이므로 각 아톰이 실세계에 대한 어떤 명제를 지시하는 것인지에 관계없이 아톰에 직접 값을 할당할 수 있다.
만일 실세계에 대한 명제의 진위 여부를 가리는
데 이용될 에이전트의 감지 장치가 신뢰할 수 있는 것이라면, 감지된 특징  의 값이 1 일 때 해당하는 명제는 참일 것이며 연관된 명제논리 아톰 (X1 이라
하자) 은 True 값을 가질 것이다. 그렇기 때문에, 감지된 정보를 입력선의 1 과 0
값으로 표시하는 대신에, 그 정보를 지식베이스 (knowledge base) 라고 하는 에이전트의
메모리 구조에 명제논리 아톰으로 표현할 수 있다. 에이전트의 지식베이스에 X1 과
같은 아톰이 나타난다는 것은 에이전트가 그 아톰에 연관된 명제가 실세계에서 사실이라고
생각한다는 것을 의미한다. 에이전트가 자신의 지식베이스에서 wff 들을 어떻게 이용하는지
곧 살펴볼 것이다.
의 값이 1 일 때 해당하는 명제는 참일 것이며 연관된 명제논리 아톰 (X1 이라
하자) 은 True 값을 가질 것이다. 그렇기 때문에, 감지된 정보를 입력선의 1 과 0
값으로 표시하는 대신에, 그 정보를 지식베이스 (knowledge base) 라고 하는 에이전트의
메모리 구조에 명제논리 아톰으로 표현할 수 있다. 에이전트의 지식베이스에 X1 과
같은 아톰이 나타난다는 것은 에이전트가 그 아톰에 연관된 명제가 실세계에서 사실이라고
생각한다는 것을 의미한다. 에이전트가 자신의 지식베이스에서 wff 들을 어떻게 이용하는지
곧 살펴볼 것이다.
어떤 해석하에서 아톰들의 값이 주어졌을 때, 진리표
(truth table) 를 이용하면 같은 해석하에서 임의의 wff 에 대한 값을 계산할 수
있다. 진리표는 연결자들의 의미를 정립한다. 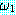 과
과 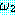 를 wff 라고 하면 진리표의 규칙은 다음과 같다.
를 wff 라고 하면 진리표의 규칙은 다음과 같다.
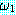 ∧
∧ 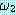 ) 는
) 는 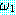 과
과 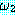 가 둘 다 True 값을 가질 때 True 이다 ; 그렇지 않으면 False 값을 갖는다.
가 둘 다 True 값을 가질 때 True 이다 ; 그렇지 않으면 False 값을 갖는다.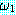 ∨
∨ 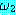 ) 는
) 는 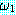 과
과 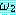 중 하나 혹은 그 이상이 True 값을 가질 때 True 이다 ; 그렇지 않으면 False
값을 갖는다.
중 하나 혹은 그 이상이 True 값을 가질 때 True 이다 ; 그렇지 않으면 False
값을 갖는다.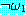 은
은 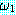 이 False 값을 가질 때 True 이다 ; 그렇지 않으면 False 값을 갖는다.
이 False 값을 가질 때 True 이다 ; 그렇지 않으면 False 값을 갖는다.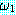 ⊃
⊃ 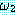 ) 는 (¬
) 는 (¬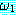 ∨
∨ 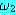 ) 의 등가 형태이다.
) 의 등가 형태이다.표 1 명제 진리표
|
|
|
|
|
|
|
| True |
True |
True |
True |
False |
True |
| True |
False |
False |
True |
False |
False |
| False |
True |
False |
True |
True |
True |
| False |
False |
False |
False |
True |
True |
위의 규칙들은 보통 표 1 과 같이 표의 형식으로 나타내므로 이들을 진리표 규칙이라고 부른다.
wff 의 구성 아톰의 값이 주어지면 진리표를 이용하여 어떤 wff 의 값도 구할 수 있다. 진리표를 이용하여 wff 의 값을 구하는 예를 들어보자. P 는 False, Q 도 False, R 은 True 라고 가정하면 [(P ⊃ Q) ⊃ R] ⊃ P 의 진리 값은 무엇인가? 안쪽에서부터 계산하면 우선 P ⊃ Q 는 True 이고 (P ⊃ Q) ⊃ R 도 True 가 된다. 마지막으로 P 가 False 이므로 전체 식은 False 가 된다.
만일 에이전트가 자신이 속한 세계를 (명제에 해당하는) n 개의 특징으로 나타내고, 이 특징들을 에이전트의 모델에서 각각에 해당하는 n 개의 아톰으로 나타낼 수 있다면, n 개의 아톰이 각각 True 아니면 False 값을 갖는 경우의 수가 2ⁿ 이므로 에이전트가 인식하는 세계는 2ⁿ 가지의 다른 상황이 있을 수 있다. 이러한 에이전트 세계의 각각의 상황이 해석 (interpretation) 에 해당한다. n 개의 아톰의 값들 (해석) 이 주어지면, 에이전트는 진리표를 이용하여 어떤 wff 의 값도 구할 수 있다. 반대의 프로세스도 가능한가? wff 의 집합에서 wff 들의 값이 주어졌다고 가정하자. 이 값들로부터 유일한 해석이 유도될 수 있는가? 종종 에이전트에게는 (True 값을 갖는 wff 들로 표현된) 특징들에 대한 제약조건들만 주어지기 때문에 이 질문은 중요한 의미를 갖는다. 그러면 에이전트는 아톰들의 값을 유도할 수 있고 따라서 실세계에 대한 해당 명제가 참인지 거짓인지 판별할 수 있을까? 즉, 주어진 식들이 실세계의 2ⁿ 가지 가능한 상황 중 하나를 지정하는가? 답은 보통 "아니오" 이다. 대신 wff 집합의 모든 wff 를 True 로 하는 해석은 여러 개 찾을 수 있다. 이 주제를 다루기 위해 모델이라는 용어를 다음 절에서 소개한다.
wff 가 주어진 해석 아래 True 이면 해석은 그 wff 를 만족시킨다 (satisfy) 고 한다. wff 를 만족시키는 해석을 그 wff 의 모델 (model) 이라고 하며 wff 집합의 각 wff 를 모두 만족시키는 해석을 그 wff 집합의 모델이라고 한다. 해석은 각 아톰에 값을 할당하는 것이므로 우리는 해석이 아톰을 만족시키는지 쉽게 알 수 있다. 그리고 나서 진리표를 이용하여 해석이 아톰들로 이루어진 wff 를 만족시키는지 알 수 있다.
앞에서 말한 블록을 들어올리는 로봇에서 특징들에 대한 제약조건은 다음 wff 로 표현되었다.
BAT_OK ∧ LIFTABLE ⊃ MOVES
위의 wff 가 True 값을 갖는다면 BAT_OK 와 LIFTABLE 이 True 이고 MOVES 가 False 인 경우는 배제되어야 한다. 각 제약조건의 wff 는 가능한 모델 중에 배제되어야 할 것들을 알려준다 (각 모델은 실세계가 처할 수 있는 여러 가지 상황 중의 하나를 나타낸다). 일반적으로 세계를 나타내는 wff 의 수가 많을수록 모델의 수는 적어진다. 실세계에 대해 아는 것이 더 많아지면 실세계가 처할 수 있는 상황에 대한 불확실성이 줄어드는 것이 당연하다.
wff (혹은 wff 집합) 를 만족시키는 해석이 없을 수도 있다. 이런 경우, 그 wff (혹은 wff 집합) 를 모순이있다 (inconsistent) 혹은 만족시킬 수 없다 (unsatisfiable) 고 말한다. 만족시킬 수 없는 wff 의 예로는 F 와 P ∧¬P 등이 있다 (어떤 해석도 이들 wff 를 만족시킬 수 없다). 만족시킬 수 없는 wff 집합의 다른 예는 {P ∨ Q, P ∨ ¬Q, ¬P ∨ Q, ¬P ∨ ¬Q} 이다 (진리표를 이용하여 어떤 해석도 모든 wff 를 True 로 만들 수 없음을 확인하라).
wff 가 구성하는 아톰의 모든 해석에 대해 True 이면 타당 (valid) 하다고 한다 (타당한 wff 는 실세계에 대한 아무런 정보도 주지 않으므로 무의미하다). 다음은 타당한 wff 의 예이다.
진리표를 이용하여 wff 의 타당성을 증명하려면 아톰값의 모든 조합에 대해 따져보아야 하므로 아톰 수에 지수적으로 비례하는 시간이 걸린다.
두 wff 의 진리값이 모든 해석에 대해 같을 때 그 두 wff 들은 동치 (equivalence) 라고 말하고 ≡ 기호로 나타낸다. 진리표를 이용하여 다음 동치 관계를 증명할 수 있다.


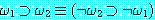
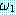 과
과 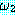 가 동치이면 다음 식은 적당하다 :
가 동치이면 다음 식은 적당하다 :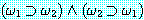
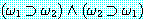 대신
대신 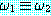 이 사용된다.
이 사용된다.wff 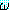 가 집합 Δ 에 있는 모든 wff 를 True 로 하는 해석에 대해 True 값을 가지면
Δ 는
가 집합 Δ 에 있는 모든 wff 를 True 로 하는 해석에 대해 True 값을 가지면
Δ 는 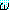 를 논리적으로 귀결한다 (logically entails) 고 하며
를 논리적으로 귀결한다 (logically entails) 고 하며 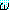 는 Δ 를 논리적으로 따른다 (logically follows) 고 한다. 그리고
는 Δ 를 논리적으로 따른다 (logically follows) 고 한다. 그리고 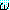 는 Δ 의 논리적 결론 (logical consequence) 이라고 한다. 논리적 귀결은 기호
는 Δ 의 논리적 결론 (logical consequence) 이라고 한다. 논리적 귀결은 기호
 를 이용하여
를 이용하여  로 표시한다.
로 표시한다.
 P
P Q
Q
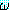 (
(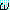 는 임의의 wff)
는 임의의 wff) P
P마지막 두 예에서는 Δ 가 단일 아톰으로 이루어진 경우 흔히 하는 대로 집합 기호를 생략하였다.
논리적 귀결은 어떤 명제들이 사실일 때 관심이 있는 다른 명제 (직접 감지될 수 없는) 의 사실 여부도 알려주는 방법을 제공하므로 인공지능 분야에서 매우 중요한 개념이다. 예를 들어, 실세계에 대한 우리의 지식을 BAT_OK ∧ LIFTABLE ⊃ MOVES 식으로 표현하고, BAT_OK 및 ¬MOVES 와 관련된 특징을 감지한다고 가정해 보자. 즉 3 개의 식이 있는데 두 개는 실세계의 특정한 상황을 나타내는 것이고 나머지 하나는 실세계에 대한 일반적인 지식을 나타내는 것이다. ¬LIFTABLE 이 이들 세 개의 식에 의해 논리적으로 귀결된다는 것을 진리표를 이용하여 각자 확인해 보기 바란다. 이러한 귀결에 따라, ¬LIFTABLE 은 세 개 식을 모두 True 가 되게 하는 모든 해석에 대해 True 이고, 따라서 우리가 의도하는 해석 (LIFTABLE 에 대한 로봇 세계와 관련된 해석) 에 대해서 True 이어야 한다. 그러므로 우리의 의도된 해석인 "블록은 들 수 없다" 라는 명제는 True 이어야 하는 것이다!
귀결은 실세계에 대한 명제의 진위 여부를 결정하는 데 매우 강력한 도구가 되므로 정보를 wff 로 표현하고 효과적으로 다른 wff 들을 귀결하는 방법을 연구하는 것은 매우 중요하다. 진리표를 이용하여 항상 이런 작업을 수행할 수 있지만, 더 간단한 방법이 있다. 귀결 (entailment) 대신 사용할 수 있는 하나의 매력적인 방법은 추론 (inference) 이다. 이들은 근본적으로는 다른 개념이지만, 정당성 (soundness) 과 완전성 (completeness) 에 의해 서로 연관된다.
추론을 귀결과 연관짓는 두 가지 정의는 다음과 같다 (이제 정리 (theorem) 와 증명 (proof), 두 단어의 직관적인 의미를 설명한다).
1. 임의의 wff 집합 Δ 와 wff 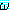 에 대해,
에 대해, 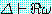 가
가  를 함의하면 (implies), 그 추론 규칙의 집합
를 함의하면 (implies), 그 추론 규칙의 집합 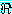 을 정당하다 (sound) 고 한다.
을 정당하다 (sound) 고 한다.
2. 임의의 wff 집합 Δ 와 wff  에 대해,
에 대해,  일 때, 추론 규칙의 집합
일 때, 추론 규칙의 집합 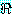 을 이용하여 Δ 로부터
을 이용하여 Δ 로부터 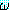 의 증명이 존재한다면,
의 증명이 존재한다면, 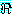 은 완전하다 (complete) 고 한다.
은 완전하다 (complete) 고 한다.
아직 명제 논리를 위한 완전한 추론 규칙의 집합에 대하여는 이야기하지 않았으며, 여기에 대해서는 다음 장에서 다룰 것이다.
추론 규칙이 정당하고 완전하면 진리표를 이용하지 않고도 증명을 탐색함으로써 한 wff 가 wff 집합을 논리적으로 따르는지 아닌지 결정할 수 있다.
추론 규칙이 정당한 경우, Δ 로부터 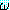 의 증명을 찾아내면
의 증명을 찾아내면 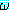 가 Δ 를 논리적으로 따르는 것이다. 추론 규칙이 완전한 경우, 증명을 찾기
위한 탐색 방법을 이용하여
가 Δ 를 논리적으로 따르는 것이다. 추론 규칙이 완전한 경우, 증명을 찾기
위한 탐색 방법을 이용하여 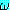 가 Δ 를 논리적으로 따르는지를 궁극적으로 확인할 수 있다. 진리표를 대신하여
증명 방법을 이용하는 것은 명제논리나 술어논리 모두에서 계산적으로 크게 유리하다
(여기에 대해서는 나중에 다룰 것이다).
가 Δ 를 논리적으로 따르는지를 궁극적으로 확인할 수 있다. 진리표를 대신하여
증명 방법을 이용하는 것은 명제논리나 술어논리 모두에서 계산적으로 크게 유리하다
(여기에 대해서는 나중에 다룰 것이다).
하나의 wff 가 어떤 wff 집합을 논리적으로 따르는지, 또는 어떤 wff 집합으로부터 증명될 수 있는지 결정하는 문제는 일반적으로 NP-hard 문제이다 [Cook 1971] (즉, 복잡도가 아톰 수에 지수적으로 비례하는 것보다 작다고 증명될 수 없는 문제이다). 그럼에도 불구하고, 계산 가능한 특수한 경우들이 있으므로 논리적인 추론 과정을 이해하는 것은 중요한 것이다.
대개의 경우 우리는 집합 Δ 의 모든 모델이 어떤 wff 의 모델임을 입증하고자 한다. 하지만 때로는 Δ 의 모델 중에서 최소 한 개만 찾으면 되는 경우도 있다. 즉, 집합 Δ 에 있는 wff 들이 모두 같은 해석에 의해 만족될 수 있다는 것을 보이고자 하는 것이다. 바꾸어 말하면, Δ 에 있는 모든 wff 의 논리곱으로 구성된 식의 모델을 찾고자 하는 것이다.
식의 모델을 구하는 문제를 명제만족성 (propositional satisfiability, PSAT) 문제라고 한다. 다음 장에서 모든 식을 리터럴의 논리합 (disjunction) 들의 논리곱 (conjunction) 으로 나타낼 수 있음을 보일 것이다. 리터럴의 논리합을 절 (clause) 이라고 부르며 절의 논리곱으로 표현된 식을 논리곱 정규형 (conjunctive normal form, CNF) 라고 한다. 그러므로 CNF 식에 대하여 PSAT 문제를 풀기만 하면 된다. 제약조건 만족, 회로 합성, 회로 진단, 계획 등의 흥미로운 문제들을 CNF PSAT 문제로 변환시켜 풀 수 있다 ([Selman, Kautz, & Cohen 1994]).
CNF PSAT 문제를 푸는 소모적인 방법은 식의 각 아톰에 True 나 False 를 할당하는 모든 경우를 다 해보면서 모든 절이 True 값을 갖는 경우가 있는지 확인하는 것이다. 식에 n 개의 아톰이 있으면 할당 방법이 2ⁿ가지 있으므로 n 이 커지면 이와 같은 소모적인 방법으로는 계산이 불가능해질 수 있다.
PSAT 문제의 두 가지 흥미있는 사례는 2SAT 과 3SAT 이다. kSAT 문제는 절이 최대 k 리터럴을 포함하는 경우에 절의 논리곱의 모델을 구하는 문제이다. 2SAT 문제는 다항 시간 (polynomial) 복잡도인 반면, 3SAT 문제는 NP-complete 이다. 그러므로 일반적인 PSAT 문제는 NP-complete 이다. 그러나 비록 PSAT 과 같이 어떤 문제에 대한 모든 알려진 알고리즘들이 최악의 경우 지수 함수적인 시간이 소요된다고 하더라도, 많은 경우에 평균 시간은 다항 시간만이 걸린다. 실제로 여러 가지 자연스러운 확률 분포에 대해서 PSAT 문제는 평균적으로 다항 시간이 걸린다 [Goldberg 1979, Purdom & Brown 1987].
GSAT 는 비소모적이고, 탐욕적인 (greedy), 언덕 오르기 (hill-climbing) 타입의 탐색 방법이다 [Selman, Levesque, & Mitchell 1992, Selman & Kautz 1993]. 이 방법은 식의 모든 아톰에 대해 무작위로 정한 값의 집합으로부터 시작한다. 이 값의 집합이 바로 해석이다. 이 해석 아래 True 값을 갖는 절의 수를 기억한다. 다음은 각 아톰을 차례로 보면서 그 아톰의 값이 변하면 몇 개의 절이 더 True 가 되는지를 계산한다. 가장 증가분이 큰 아톰의 값을 변경시키고 이와 같은 작업을 계속한다. 물론 가장 큰 증가분이 0 이나 음수가 될 수도 있지만 GSAT 은 어떤 경우에도 한 아톰의 값을 변경한다. 이 절차는 평원 (plateau) 에서 끝없이 헤맬 수도 있으므로, 일정한 수만큼의 변경을 하고 나면 종료한다. 또한 이 절차는 지역 최대값 (local maximum, 일부의 절만 만족하는 해석) 에서 종료될 수 있으므로, 이럴 때는 더 나은 최대값을 찾기 위해 다른 무작위 해석에서 다시 시작해야 할 수도 있다. GSAT 는 2000 개의 변수를 가진 무작위로 생성된 3SAT 문제에 대해 모델을 찾을 수 있었으며, 방대한 N-퀸 문제를 명제로 변환한 문제를 푸는 데에도 이용되었다. 임의 진행 형태로 GSAT 를 수정한 WALKSAT 과 같은 알고리즘은 효과를 향상시킨다는 것이 확인되었다 [Selman, Kautz & Cohen 1994, Selman, Kautz & Cohen 1996].
명제논리는 인공 에이전트가 자신의 세상을 표현하기
위해 사용하는 공식적인 언어이다. 혹시 수학과 자연언어 (명제논리를 설명하기 위해
이 책에서 사용하고 있는) 의 비공식적인 언어를 명제논리 자체의 공식적인 언어와
혼동할 수도 있다. 예를 들어, {P, P ⊃ Q} ├ Q 라고 말할 때, 우리는 기호
├ 를 사용한다. 이 기호는 명제논리 언어의 기호가 아니고 명제논리를 이야기하기
위해 사용되는 우리 언어의 기호이다. 메타 언어 기호 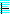 나
나  를 기호 ⊃ 와 혼동하면 안된다.
를 기호 ⊃ 와 혼동하면 안된다.
명제논리의 정리 (추론 규칙에 의해 생성되는) 이외에 명제논리에 대한 정리가 있는데 이를 메타정리 (metatheorem) 라고 부른다. 다음은 명제논리에 대한 중요한 두 가지 정리이다.
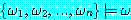 이면
이면 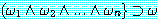 는 정당하며,
는 정당하며, 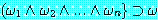 가 정당하면
가 정당하면 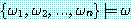 이다.
이다.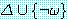 는 없으면 (즉, 합집합의 모든 wff 를 만족시키는 해석이 없으면),
는 없으면 (즉, 합집합의 모든 wff 를 만족시키는 해석이 없으면),  이다.
이다. 2항 연결자 ∧ 과 ∨ 는 결합 법칙이 성립된다. 즉,
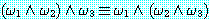
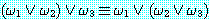
그러므로 위의 wff 에서 괄호를 빼고 다음과 같이 쓸 수 있다.
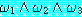
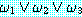
처음 것을 논리곱 (conjunction), 두번째를 논리합
(disjunction) 이라고 한다. 처음 wff 에 있는 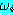 들을 논리곱 인자 (conjunct) 라고 하며, 두 번째 wff 에 있는 것들을 논리합
인자 (disjunct) 라고 한다.
들을 논리곱 인자 (conjunct) 라고 하며, 두 번째 wff 에 있는 것들을 논리합
인자 (disjunct) 라고 한다.