술어논리
논리융합
(Resolution
in the Predicate
Calculus)
인공지능-지능형
에이전트를 중심으로
: Nils
J.Nilsson 저서, 최중민. 김준태. 심광섭. 장병탁 공역, 사이텍미디어, 2000
(원서 : Artificial Intelligence :
A New Synthesis 1998), Page 271~285
1. 단일화
2. 술어논리 논리융합
3. 완전성과 정당성
4. 임의 정형식을 절 형태로 변환하기
5. 논리융합을 이용한 정리증명
6. 답변 추출
7. 동등 술어
8. 참고문헌 및 토론
이 책에서는 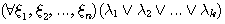 와 같은 정형식을
와 같은 정형식을 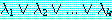 로 줄여서 표현할 때도 있는데 여기서
로 줄여서 표현할 때도 있는데 여기서 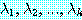 는 변수
는 변수 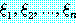 을 포함하고 있는 리터럴을 나타낸다. 이와 같이 전체 한정사를 생략하고 표현하는
경우에
을 포함하고 있는 리터럴을 나타낸다. 이와 같이 전체 한정사를 생략하고 표현하는
경우에 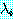 에서 사용된 변수는 전체 한정사에 의해 한정을 받는 것으로 가정한다 (이렇게
하기 위해서는 존재 한정사에 의해 한정받는 변수들을 먼저 제거해야 하는데 이에
대해서는 뒤에서 설명하기로 한다). 이와 같이 간단하게 표현한 정형식을 절 (clause)
이라고 한다. 하나의 절을
에서 사용된 변수는 전체 한정사에 의해 한정을 받는 것으로 가정한다 (이렇게
하기 위해서는 존재 한정사에 의해 한정받는 변수들을 먼저 제거해야 하는데 이에
대해서는 뒤에서 설명하기로 한다). 이와 같이 간단하게 표현한 정형식을 절 (clause)
이라고 한다. 하나의 절을 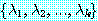 와 같은 집합형식으로 표현하기도 하는데 이런 경우 각 원소들이 논리합으로
연결되어 있는 것으로 가정한다.
와 같은 집합형식으로 표현하기도 하는데 이런 경우 각 원소들이 논리합으로
연결되어 있는 것으로 가정한다.
두 절이 똑같은 리터럴을 포함하고 있으면서 각
리터럴이 서로 상반 (complementary) 된 경우 명제논리에서와 마찬가지로 이 둘을
논리융합 (resolution) 할 수 있다. 예를 들어, 어떤 절에 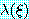 란 리터럴이 포함되어 있고 (ξ 는 변수임), 또 다른 절에 ¬λ(τ) 란 상반된
리터럴이 포함되어 있으며, τ 가 ξ 를 포함하지 않는 항이면, 첫번째 절에서 ξ
를 τ 로 치환한 후 상반된 리터럴에 대한 명제논리에서의 논리융합을 수행함으로써
두 절에 대한 논리융합식 (resolvent) 을 생성할 수 있다.
란 리터럴이 포함되어 있고 (ξ 는 변수임), 또 다른 절에 ¬λ(τ) 란 상반된
리터럴이 포함되어 있으며, τ 가 ξ 를 포함하지 않는 항이면, 첫번째 절에서 ξ
를 τ 로 치환한 후 상반된 리터럴에 대한 명제논리에서의 논리융합을 수행함으로써
두 절에 대한 논리융합식 (resolvent) 을 생성할 수 있다.
예 : 두 절 P(f(y), A)
∨ Q(B, C) 와 ¬P(x, A) ∨ R(x, C) ∨ S(A, B) 가 있다고 하자. 두번째 절에서
x 를 f(y) 로 치환하면 ¬P(f(y), A) ∨ R(f(y), C) ∨ S(A, B) 가 된다. 그러면
두번째 절의 첫번째 리터럴은 첫번째 리터럴과 정확히 상반된 꼴이다. 따라서 이
리터럴에 대하여 논리융합을 수행하면 R(f(y), C) ∨ S(A, B) ∨ Q(B, C) 라는 논리융합식을
얻게 된다.
이러한 치환은 단일화 (unification) 라는 과정에
의해 이루어진다. 단일화는 인공지능에서 매우 중요한 개념이다. 단일화에 대하여
설명하기 전에 치환에 대한 일반적인 사항에 대하여 살펴보자.
정형식의 각 항은 변수, 객체상수, 또는 함수식
등이 가능하다. 여기서 함수식이란 함수상수와 항으로 이루어진 것을 의미한다. 어떤
정형식에 대한 치환 사례 (substitution instance) 는 그 정형식에 나타난 변수를
항으로 치환함으로써 얻을 수 있다. 예를 들어 P[x, f(y), B] 에 대한 4 가지 치환
사례는 다음과 같다.
P[z, f(w), B]
P[x, f(A), B]
P[g(z), f(A), B]
P[C, f(A), B]
첫번째 치환 사례는 P[x, f(y), B] 에 나타난 변수를
단순히 다른 변수로 치환함으로써 얻어진 것으로서 알파벳 변이 (alphabetic variant)
라고 부른다. 네번째 치환 사례에서는 리터럴을 이루고 있는 항에 아무런 변수가
포함되어 있지 않은 것으로서 기초 사례 (ground instance) 라고 부른다 (기초 항
(ground term) 은 아무런 변수도 포함하고 있지 않은 항을 말한다).
치환을 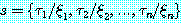 과 같은 순서쌍의 집합으로 나타낼 수도 있다. 순서쌍
과 같은 순서쌍의 집합으로 나타낼 수도 있다. 순서쌍 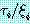 는 치환이 미치는 범위내에 있는 변수
는 치환이 미치는 범위내에 있는 변수 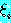 모두를 항
모두를 항 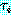 로 바꾸는 것을 의미한다. 어떤 변수를 치환할 때 같은 변수를 포함하고 있는
항과 치환할 수는 없다. 위의 P[x, f(y), B] 에 대한 치환 사례를 얻는 데 사용된
치환은 다음과 같다.
로 바꾸는 것을 의미한다. 어떤 변수를 치환할 때 같은 변수를 포함하고 있는
항과 치환할 수는 없다. 위의 P[x, f(y), B] 에 대한 치환 사례를 얻는 데 사용된
치환은 다음과 같다.
s1 = {z/x, w/y}
s2 = {A/y}
s3 = {g(z)/x, A/y}
s4 = {C/x, A/y}
이 책에서는 어떤 식 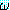 를 s 로 치환한 치환 사례를
를 s 로 치환한 치환 사례를 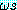 와 같이 표기하기로 한다. 그러므로 P[z, f(w), B] 는 P[x, f(y), B]s1 과 같다.
s1 과 s2 에 대한 합성은 s1s2 로 표기하는데 이것은 s1 의 각 항에 s2 를 적용하고
여기에 s1 에서 나타나지 않고 s2 에서만 나타난 변수를 추가하여 만든 치환을 의미한다.
그러므로 {g(x, y)/z}{A/x, B/y, C/w, D/z} 은 {g(A, B)/z, A/x, B/y, C/w} 와 같다.
어떤 식
와 같이 표기하기로 한다. 그러므로 P[z, f(w), B] 는 P[x, f(y), B]s1 과 같다.
s1 과 s2 에 대한 합성은 s1s2 로 표기하는데 이것은 s1 의 각 항에 s2 를 적용하고
여기에 s1 에서 나타나지 않고 s2 에서만 나타난 변수를 추가하여 만든 치환을 의미한다.
그러므로 {g(x, y)/z}{A/x, B/y, C/w, D/z} 은 {g(A, B)/z, A/x, B/y, C/w} 와 같다.
어떤 식 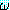 에 s1 과 s2 를 연속해서 적용하는 것은
에 s1 과 s2 를 연속해서 적용하는 것은 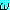 에 s1s2 를 적용하는 것과 같다. 따라서
에 s1s2 를 적용하는 것과 같다. 따라서 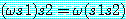 의 관계가 성립한다. 치환 합성은 결합 법칙이 성립한다. 따라서 (s1s2)s3 =
s1(s2s3) 의 관계가 성립한다.
의 관계가 성립한다. 치환 합성은 결합 법칙이 성립한다. 따라서 (s1s2)s3 =
s1(s2s3) 의 관계가 성립한다.
예 : 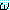 를 P(x, y), s1 을 {f(y)/x}, s2 를 {A/y} 라고 하자. 그러면
를 P(x, y), s1 을 {f(y)/x}, s2 를 {A/y} 라고 하자. 그러면
(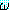 s1)s2 = [P(f(y), y)]{A/y} = P(f(A), A)
s1)s2 = [P(f(y), y)]{A/y} = P(f(A), A)
이고
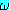 (s1s2) = [P(x, y)]{f(A)/x, A/y} = P(f(A), A)
(s1s2) = [P(x, y)]{f(A)/x, A/y} = P(f(A), A)
이다.
일반적으로 치환은 교환 법칙이 성립하지 않는다.
즉, 일반적으로 s1s2 = s2s1 의 관계가 성립하지 않는다. 그러므로 치환을 적용하는
순서는 중요하다.
예 : (위의 예에서 사용한
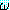 , s1, s2 를 여기서도 사용한다.)
, s1, s2 를 여기서도 사용한다.)
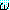 (s1s2) = P(f(A), A)
(s1s2) = P(f(A), A)
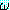 (s2s1) = [P(x, y)]{A/y, f(y)/x} = P(f(y), A)
(s2s1) = [P(x, y)]{A/y, f(y)/x} = P(f(y), A)
정형식의 집합 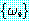 의 모든 원소에 대하여 치환 s 를 적용하는 경우에는 이것을
의 모든 원소에 대하여 치환 s 를 적용하는 경우에는 이것을 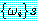 로 표기하기로 한다.
로 표기하기로 한다. 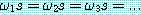 의 관계가 성립하는 치환 s 가 존재하는 경우 정형식의 집합
의 관계가 성립하는 치환 s 가 존재하는 경우 정형식의 집합 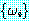 는 단일화가 가능하다 (unifiable) 고 한다. 이러한 경우 치환 s 를
는 단일화가 가능하다 (unifiable) 고 한다. 이러한 경우 치환 s 를 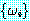 의 단일자 (unifier) 라고 한다. 예를 들어, 치환 s = {A/x, B/y} 는 정형식의
집합 {P[x, f(y), B], P[x, f(B), B]} 를 {P[A, f(B), B]} 로 단일화한다. 비록 치환
s = {A/x, B/y} 는 정형식의 집합 {P[x, f(y), B], P[x, f(B), B]} 에 대한 단일자이지만
이것이 가장 간단한 형태의 단일자는 아니다. 예를 들어, 위에서 x 를 A 로 치환하지
않더라도 단일화를 할 수 있다. 정형식의 집합
의 단일자 (unifier) 라고 한다. 예를 들어, 치환 s = {A/x, B/y} 는 정형식의
집합 {P[x, f(y), B], P[x, f(B), B]} 를 {P[A, f(B), B]} 로 단일화한다. 비록 치환
s = {A/x, B/y} 는 정형식의 집합 {P[x, f(y), B], P[x, f(B), B]} 에 대한 단일자이지만
이것이 가장 간단한 형태의 단일자는 아니다. 예를 들어, 위에서 x 를 A 로 치환하지
않더라도 단일화를 할 수 있다. 정형식의 집합 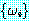 의 가장 일반적인 (또는 가장 단순한) 단일자 (most general unifier, mgu 라고
함) g 는 다음과 같은 성질을 가지고 있다. 치환 s 에 의해 정형식의 집합
의 가장 일반적인 (또는 가장 단순한) 단일자 (most general unifier, mgu 라고
함) g 는 다음과 같은 성질을 가지고 있다. 치환 s 에 의해 정형식의 집합 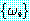 가
가 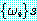 로 단일화되면
로 단일화되면  의 관계가 성립하는 치환 s' 이 존재한다. 또한 가장 일반적인 단일자에 의해
생성된 치환 결과는 알파벳 변이를 제외하고는 유일하다.
의 관계가 성립하는 치환 s' 이 존재한다. 또한 가장 일반적인 단일자에 의해
생성된 치환 결과는 알파벳 변이를 제외하고는 유일하다.
유한 크기의 정형식의 집합에 대하여 단일화가
가능한 경우에는 가장 일반적인 단일자를 찾아주고 그렇지 않은 경우에는 단일화가
불가능하다는 사실을 알려주는 알고리즘은 많이 있다. 이 책에서 소개하는 UNIFY
알고리즘은 [Chang & Lee 1973, p.77] 에 나온 알고리즘을 수정한 것이다. 이
알고리즘에서는 리터럴과 항이 리스트 형식으로 표현된 정형식의 집합으로 주어지는
것을 가정하고 있다. 리터럴 ¬P(x, f(A, y)) 를 리스트 형식으로 나타내면 (¬P
x (f A y)) 와 같다. P 는 첫번째 레벨의 식이며 (f A y) 는 세번째 레벨의 식이다.
UNIFY 알고리즘의 기초는 불일치 집합 (disagreement
set) 이라는 개념이다. 공집합이 아닌 정형식의 집합 W 에 대한 불일치 집합을 얻기
위해서는 우선 W 에 속하는 정형식에 사용된 기호 중 서로 일치하지 않는 제일 왼쪽
기호를 찾은 다음 W 에서 이 위치에 나오는 기호로 시작하는 부분식을 추출하면 된다.
각 부분식의 집합이 W 에 대한 불일치 집합이 된다. 예를 들어, 두 개의 리스트로
이루어진 정형식의 집합 {(¬P x (f A y)), (¬Px (f z B)} 에 대한 불일치 집합은
{A, z} 이다. 이러한 불일치는 치환 A/z 에 의해 해소될 수 있다.
UNIFY (Γ) (Γ 는 리스트로 표현된 정형식의 집합을
나타낸다.)
UNIFY 는 단일화가 가능한 정형식의 집합에 대해서는
가장 일반적인 단일자를 발견하며 단일화가 불가능한 정형식의 집합에 대해서는 단일화에
실패했음을 알려준다는 사실이 [Chang & Lee 1973, p.79] 에 증명되어 있다.
이 단일화 알고리즘에 의해 생성된 mgu 는 리스트 형식의 정형식의 쌍으로 표현되어
있지만 이것을 일차 술어논리에서 사용하는 형식으로 바꾸는 것은 매우 간단하다.
그 밖에도 단일화를 수행하는 몇 가지 다늘 알고리즘들이 있다. 이 중에는 선형 시간
(linear time) 복잡도를 가지고 단일화를 수행하는 것도 있다 [Paterson & Wegman
1978].
다음은 몇 개의 리터럴 집합에 대한 가장 일반적인
치환 사례를 보인 것이다. 이들 리터럴 집합에 대하여 UNIFY 알고리즘을 직접 적용해
보기 바란다.
|
리터럴
집합
|
가장
일반적인 치환 사례
|
|
{P(x),
P(A)}
{P[f(x),
y, g(y)], P[f(x), z, g(x)]}
{P[f(x,
g(A, y)), g(A, y)], P[f(x, z), z]}
|
P(A)
P[f(x),
x, g(x)]
P[f(x,
g(A, y)), g(A, y)]
|
UNIFY 알고리즘의 단계 4 에서 우리는 어떤 변수가
치환하고자 하는 항에 변수가 어떤 항에 나타나는가를 검사하였다. 이러한 검사를
하지 않고 모든 치환을 허용할 경우 단일화 과정이 무한히 반복될 우려가 있다. 예를
들어 P(x, x) 와 P(f(z), z) 를 단일화한다고 하자. UNIFY 알고리즘에 따라 이 식에서
사용된 x 는 f(z) 로 치환되어 P(f(z), f(z)) 와 P(f(z), z) 가 생성될 것이다. 그러나
아무런 검사를 하지 않을 경우 z 는 f(z) 로 치환할 수 있는데 이 경우 P(f(f(z)),
f(f(z))) 와 P(f(f(z)), f(z)) 가 생성되는데 이러한 과정은 무한히 반복된다.
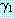 과
과 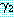 를 각각 리터럴의 집합으로 표현된 절이라고 하자.
를 각각 리터럴의 집합으로 표현된 절이라고 하자. 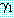 에 아톰
에 아톰 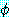 가 있고
가 있고 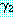 에 리터럴
에 리터럴 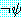 가 있을 때
가 있을 때 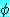 와
와 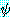 가 mgu
가 mgu 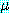 를 가지고 있다면 이 두 절은 논리융합식
를 가지고 있다면 이 두 절은 논리융합식 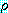 를 가진다. 논리융합식은
를 가진다. 논리융합식은 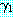 과
과 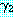 의 합집합에 치환
의 합집합에 치환 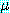 를 적용함으로써 얻어진다. 즉,
를 적용함으로써 얻어진다. 즉,
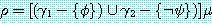
변수에 대한 혼란을 피하기 위해 두 절을 논리융합하기
전에 각 절에 있는 변수 이름이 중복되지 않도록 변수 이름을 변경한다. 예를 들어
P(x) ∨ Q(f(x)) 와 R(g(x)) ∨ ¬Q(f(A)) 를 논리융합한다고 하자. 먼저 두번째
절을 R(g(y)) ∨ ¬Q(f(A)) 로 변경한 후 논리융합을 수행하면 P(A) ∨ R(g(y)) 를
얻는다. 변수 이름을 변경하는 것을 변수 표준화 (standardizing the variables apart)
라고 한다. 다음 예를 보자.
P(x), Q(x, y) 와 {¬P(A), R(B, z)} 를 논리융합하면
{Q(A, y), R(B, z)} 를 얻는다.
{P(x, x), Q(x), R(x)} 와 {¬P(A, z), ¬Q(B)}
를 논리융합하는 방법은 두 가지인데 각각 {Q(A), R(A), Q(B)} 와 {¬P(B, B), R(B),
¬P(A, z)} 를 얻는다.
술어논리 논리융합에 대하여 보다 강력한 정의가
필요할 때가 있다. 두 절 {P(u), P(v)} 와 {P(x), ¬P(y)} 를 예로 들어보자. 이
두 절은 각각 (A/u, A/v, A/x, A/y 에 의해 얻어진) P(A), ¬P(A) 와 동치인 기초
사례를 가진다. 이 기초 사례로부터 공절 (empty clause) 을 추론할 수 있다. 따라서
원래 주어진 절로부터 공절을 추론할 수도 있어야 한다. 그러나 앞에서 제시한 논리융합
방법으로는 이러한 추론을 할 수가 없다. 논리융합에 대한 보다 강력한 규칙은 다음과
같다.
위에서와 마찬가지로 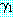 과
과 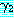 를 각각 리터럴의 집합으로 표현한 절이라고 하자.
를 각각 리터럴의 집합으로 표현한 절이라고 하자. 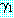 과
과 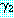 를 각각
를 각각 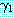 ,
, 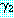 의 부분집합이라고 했을 때 mgu
의 부분집합이라고 했을 때 mgu 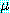 를 사용하여
를 사용하여 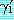 의 리터럴들과
의 리터럴들과 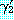 의 리터럴들의 부정을 단일화시킬 수 있다면 이 두 절은 논리융합식
의 리터럴들의 부정을 단일화시킬 수 있다면 이 두 절은 논리융합식 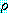 를 가진다. 이 논리융합식은
를 가진다. 이 논리융합식은 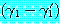 과
과 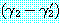 의 합집합에 치환
의 합집합에 치환 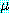 를 적용함으로써 얻어진다. 즉,
를 적용함으로써 얻어진다. 즉,
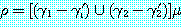
이러한 정의에 따라 두 절 {P(u), P(v)} 와 {¬P(x),
¬P(y)} 를 논리융합하면 공절을 얻게 된다.
술어논리에서의 논리융합은 정당 (sound) 하다.
즉, 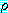 가 두 절
가 두 절 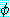 와
와 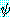 의 논리융합식이라면
의 논리융합식이라면 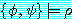 이다. 이것을 증명하는 것은 명제논리에서의 논리융합에 대한 정당성 (soundness)
을 증명하는 것보다 어렵지 않다. 논리융합만으로는 주어진 정형식의 집합으로부터
논리적으로 귀결 (logically entail) 되는 모든 식을 추론할 수 없다. 예를 들어,
P(A) 로부터 P(A) ∨ P(B) 를 추론할 수 없다. 명제논리에서의 논리융합에서는 논리융합
반박 (resolution refutation) 을 이용하여 이러한 문제점을 극복하였는데 술어논리에서도
마찬가지로 할 수 있다. 그러나 반박의 완전성 (completeness) 을 보장하기 위해서는
논리융합에 대한 보다 강력한 정의를 이용해야 한다.
이다. 이것을 증명하는 것은 명제논리에서의 논리융합에 대한 정당성 (soundness)
을 증명하는 것보다 어렵지 않다. 논리융합만으로는 주어진 정형식의 집합으로부터
논리적으로 귀결 (logically entail) 되는 모든 식을 추론할 수 없다. 예를 들어,
P(A) 로부터 P(A) ∨ P(B) 를 추론할 수 없다. 명제논리에서의 논리융합에서는 논리융합
반박 (resolution refutation) 을 이용하여 이러한 문제점을 극복하였는데 술어논리에서도
마찬가지로 할 수 있다. 그러나 반박의 완전성 (completeness) 을 보장하기 위해서는
논리융합에 대한 보다 강력한 정의를 이용해야 한다.
명제논리에서와 같이 임의의 정형식을 다음과 같은
단계에 따라 절 형태 (clause form) 로 변환할 수 있다.
1. (명제논리에서
그랬듯이) 함의 (implication) 를 나타내는 부호를 제거한다.
2. (명제논리에서
그랬듯이) 부정을 나타내는 부호의 범위를 줄인다.
3. 변수
표준화를 한다. 각 한정사가 한정하는 변수의 이름이 유일하도록 변수명을 바꾼다.
예
: (∀x)[¬P(x) ∨ (∃x)Q(x)] 를 (∀x)[¬P(x) ∨ (∃y)Q(y)] 로 바꾼다.
4. 존재
한정사를 제거한다.
예
: (∀x)[(∃y) Height (x, y)] 에서 존재 한정사는 전체 한정사의 범위내에 있다.
따라서 y 는 x 의 값에 의존하게 된다. 예를 들어 (∀x)[(∃y) Height (x, y)]
가 "모든 사람 x 의 키가 y 이다" 라는 것을 의미한다고 하자. 키는
사람에 따라 달라지는데 이러한 의존 관계가 미지의 함수 h(x) 에 의해 명시적으로
주어진다고 하자. 이 함수는 x 를 실존하는 y 로 사상시켜 주는 함수인데 이러한
함수를 Skolem 함수라고 한다. y 대신 Skolem 함수를 사용한다면 존재 한정사를
제거할 수 있다. 이러한 방법으로 (∀x)[(∃y) Height (x, y)] 는 (∀x)[Height
(x, h (x))] 로 바꾸어 표현할 수 있다.
정형식에서
존재 한정사를 제거하는 일반적인 규칙은 존재 한정사에 의해 한정을 받는 변수
Skolem 함수로 대치하는 것이다. 여기서 사용된 Skolem 함수의 인자는 현재 제거중인
존재 한정사의 범위를 포함하는 전체 한정사에 의해 한정을 받는 변수들로 이루어진다.
Skolem 함수를 나타내는 데 사용되는 함수 기호는 주어진 논리융합 반박에 사용될
정형식에 나타나지 않은 것이어야 한다.
이러한
방법에 따라 다음 정형식에서
[(∀w)Q(w)]
⊃ (∀x){(∀y){(∃z)[P(x, y, z) ⊃ (∀u)R(x, y, u, z)]}}
(∃z)
를 제거하면 다음과 같다.
[(∀w)Q(w)]
⊃ (∀x){(∀y)P(x, y, g(x, y)) ⊃ (∀u)R(x, y, u, g(x, y))]}
마찬가지로
다음 정형식에서
(∀x){¬P(x)
∨ {(∀y)[¬P(y) ∨ P(f(x, y))] ∧ (∃w)[Q(x, w) ∧ ¬P(w)]}}
(∃w)
를 제거하면 다음과 같다.
*(∀x){¬P(x)
∨ {(∀y)[¬P(y) ∨ P(f(x, y))] ∧ [Q(x, h(x)) ∧ ¬P(h(x))]}}
여기서
g(x, y) 와 h(x) 는 Skolem 함수이다.
제거중인
존재 한정사가 전체 한정사의 범위 밖에 있다면 이것을 제거하기 위해 인자가
없는 Skolem 함수 즉, 상수를 사용한다. 따라서 (∃x)P(x) 는 P(Sk) 가 된다.
여기서 상수 기호 sk 는 우리가 존재하는 것으로 알고 있는 사물을 나타내는데
이는 다른 정형식에서 사용되지 않은 것이어야 한다.
정형식에서
존재 한정사에 의해 한정받는 모든 변수를 제거하려면 정형식의 각 부분에 대하여
위의 절차를 적용하면 된다. 정형식의 집합으로부터 존재 한정사를 제거하면
정형식의 집합에 대한 소위 Skolem 형식 (Skolem form) 을 얻을 수 있다.
정형식에
대한 Skolem 형식은 처음 주어진 정형식과 동치가 아니라는 사실에 주의해야
한다. 예를 들어 (∃x)P(x) 로부터 P(Sk) 라는 Skolem 형식이 논리적으로 귀결
(logically entail) 된다. 그러나 역은 성립하지 않는다. 또 다른 예로서 [P(A)
∨ P(B)]  (∃x)P(x) 가 성립하지만 [P(A) ∨ P(B)]
(∃x)P(x) 가 성립하지만 [P(A) ∨ P(B)] 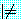 P(Sk) 는 성립하지 않는다. 정형식의 집합 Δ 은 Δ 의 Skolem 형식이 만족 가능할
때에 한하여 만족 가능하다고 한다. 또는 Δ 의 Skolem 형식이 만족 불가능할
때에 한하여 Δ 는 만족 불가능 (unsatisfiable) 하다고 한다 [Loveland 1978,
pp.41ff].
P(Sk) 는 성립하지 않는다. 정형식의 집합 Δ 은 Δ 의 Skolem 형식이 만족 가능할
때에 한하여 만족 가능하다고 한다. 또는 Δ 의 Skolem 형식이 만족 불가능할
때에 한하여 Δ 는 만족 불가능 (unsatisfiable) 하다고 한다 [Loveland 1978,
pp.41ff].
5. Prenex
형식으로 변경한다. 이 단계에서 존재 한정사는 더 이상 존재하지 않으며 전체
한정사는 자기 자신의 변수를 가지게 된다. 이제 모든 전체 한정사를 정형식의
제일 앞으로 이동시킨다. 이 경우, 각 한정사의 범위는 정형식 전체가 된다.
이렇게 해서 얻은 정형식을 prenex 형식이라고 한다. prenex 형식으로 주어진
정형식은 접두사 (prefix) 라고 하는 일련의 한정사와 이 뒤에 나오는 행렬 (matrix)
이라고 하는 한정사가 없는 식으로 이루어진다. 앞의 예에서 * 표로
표시한 정형식의 prenex 형식은 다음과 같다.
(∀x)(∀y){¬P(x)
∨ {[¬P(y) ∨ P(f(x, y))] ∧ [Q(x, h(x)) ∧ ¬P(h(x))]}}
6. 명제논리에서와
마찬가지로 행렬을 논리곱 정규형 (conjunctive normal form) 으로 변형한다.
행렬은 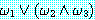 을
을 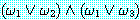 로 대치하는 분배 법칙을 계속 적용함으로써 논리곱 정규형으로 변형된다.
로 대치하는 분배 법칙을 계속 적용함으로써 논리곱 정규형으로 변형된다.
앞에서
예로 든 정형식에 대한 행렬을 논리곱 정규형으로 변형하면 다음과 같다.
(∀x)(∀y){[¬P(x)
∨ ¬P(y) ∨ P(f(x, y))] ∧ [¬P(x) ∨ Q(x, h(x))] ∧ [¬P(x) ∨ ¬P(h(x))]}
7. 전체
한정사를 제거한다. 정형식에서 사용된 모든 변수는 한정사의 범위내에 있어야
하므로 현재까지 남아있는 모든 변수는 전체 한정사에 의해 한정을 받음을 확실히
알 수 있다. 또한 전체 한정사의 순서는 별로 중요하지 않다. 그러므로 전체
한정사를 명시적으로 표시하지 않더라도 행렬에 사용된 모든 변수는 전체 한정사에
의해 한정을 받는다고 가정할 수 있다. 이렇게 하면 논리곱 정규형으로 주어진
행렬을 얻을 수 있다.
8. 논리곱
∧ 기호를 제거한다. 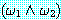 형식으로 주어진 식을 정형식의 집합
형식으로 주어진 식을 정형식의 집합 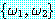 로 대치함으로써 논리곱 기호를 제거할 수 있다. 이러한 절차를 반복하면 정형식의
유한집합을 얻을 수 있다. 여기서 각 정형식은 리터럴의 논리곱이다. 리터럴들의
논리합만으로 이루어진 정형식을 절 (clause) 이라고 불린다. 이 책에서 예로
든 정형식은 다음과 같은 절의 집합으로 변형된다.
로 대치함으로써 논리곱 기호를 제거할 수 있다. 이러한 절차를 반복하면 정형식의
유한집합을 얻을 수 있다. 여기서 각 정형식은 리터럴의 논리곱이다. 리터럴들의
논리합만으로 이루어진 정형식을 절 (clause) 이라고 불린다. 이 책에서 예로
든 정형식은 다음과 같은 절의 집합으로 변형된다.
9. 변수
이름을 변경한다. 하나의 변수 기호가 두 개 이상의 절에 나타나지 않도록 변수
기호의 이름을 변경할 수 있다. (∀x)[P(x) ∧ Q(x)] 은 [(∀x)P(x) ∧ (∀y)Q(y)]
와 동치이다. 위의 절에서 사용된 변수명을 변경하면 다음과 같다.
정리증명 시스템 (theorem-proving system) 에서
논리융합을 추론 규칙으로 사용한다면 정형식 (여기서부터 이론을 증명하려고 한다)
은 우선 절로 변형된다. 정형식 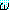 가 정형식의 집합 Δ 로부터 논리적으로 유도된다면 정형식
가 정형식의 집합 Δ 로부터 논리적으로 유도된다면 정형식 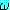 는 Δ 에 속한 정형식을 절로 변형하여 얻은 절의 집합으로부터도 논리적으로
유도되며 역도 성립한다 [Davis & Putnam 1960]. 따라서 절은 술어논리에서의
정형식을 표현하는 일반적인 형식이다.
는 Δ 에 속한 정형식을 절로 변형하여 얻은 절의 집합으로부터도 논리적으로
유도되며 역도 성립한다 [Davis & Putnam 1960]. 따라서 절은 술어논리에서의
정형식을 표현하는 일반적인 형식이다.
논리융합 반박의 완전성과 정당성을 보일 수 있다
[Robinson 1965]. ([Chang & Lee 1973, p.85] 참조) 그러므로 Δ 로부터 정형식
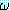 을 증명하는 것은 명제논리에서의 증명방법과 같다. 즉,
을 증명하는 것은 명제논리에서의 증명방법과 같다. 즉, 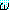 를 부정한 다음 이것을 절로 변형하고 이것을 Δ 의 절에 추가한다. 그리고 나서
공절이 연역적으로 추론 (deduce) 될 때까지 논리융합을 적용한다. 명제논리에서의
논리융합에 대한 설명을 하면서 소개한 순서 (ordering) 와 개선 전략 (refinement
strategy) 을 사용할 수도 있다.
를 부정한 다음 이것을 절로 변형하고 이것을 Δ 의 절에 추가한다. 그리고 나서
공절이 연역적으로 추론 (deduce) 될 때까지 논리융합을 적용한다. 명제논리에서의
논리융합에 대한 설명을 하면서 소개한 순서 (ordering) 와 개선 전략 (refinement
strategy) 을 사용할 수도 있다.
짐꾸러미를 운반하는 로봇을 예로 들어보자. 이
로봇은 27 번 방에 있는 모든 짐꾸러미가 28 번 방에 있는 것보다 작다는 것을 알고
있다고 하자. 따라서
1. (∀x,
y)[Package(x) ∧ Package(y) ∧ Inroom(x, 27) ∧ Inroom(y, 28)] ⊃ Smaller(x,
y)
술어
기호를 단축하여 윗식을 보다 간결하게 표현한 후 절의 형태로 변형하면 다음과
같다.
2. ¬P(x)
∨ ¬P(y) ∨ ¬I(x, 27) ∨ ¬I(y, 28) ∨ S(x, y)
로봇이
어느 방인지는 모르지만 27 번 방 아니면 28 번 방에 짐꾸러미 A 가 있다는 사실을
알고 있다고 하자. 이 로봇은 짐꾸러미 B 가 27 번 방에 있으며, 짐꾸러미 B
는 짐꾸러미 A 보다 작지 않다는 것을 알고 있다.
3. P(A)
4. P(B)
5. I(A,
27) ∨ I(A, 28)
6. I(B,
27)
7. ¬S(B,
A)
논리융합 반박을 사용하여 이 로봇은 짐꾸러미
A 가 27 번 방에 있다는 것을 증명할 수 있다. 이 증명에 대한 증명트리 (proof tree)
는 그림 1 과 같다. 증명할 정형식에 대한 부정은 좌측 상단에 있다. 로봇이 알고
있는 사실에 해당하는 정형식은 이 그림에서 우측에 나타내었다. 이 그림에서는 논리융합에
사용된 치환도 함께 나타내었다.

그림 1 논리융합 반박
논리융합을 이용하여 술어논리 정형식으로 표현된
도메인에 관한 지식을 사용하여 주어진 질의에 대한 답을 구하는 것은 주어진 정리를
증명하는 것보다 더 어렵다. 예를 들어 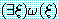 와 같은 형태의 정리를 증명한다고 가정해 보자. 이미 존재하는 것으로 증명된
ξ 를 생성하려 하는 경우도 있을 것이다. 이를 위해서는 반박 과정 중에 적용된
치환을 기억하고 있어야 한다. 이러한 치환은 답변 리터럴 (answer literal) 이라는
형식으로 기억할 수 있다. 증명하고자 하는 정리에 대한 부정으로부터 만들어진 각
절에 Ans
와 같은 형태의 정리를 증명한다고 가정해 보자. 이미 존재하는 것으로 증명된
ξ 를 생성하려 하는 경우도 있을 것이다. 이를 위해서는 반박 과정 중에 적용된
치환을 기억하고 있어야 한다. 이러한 치환은 답변 리터럴 (answer literal) 이라는
형식으로 기억할 수 있다. 증명하고자 하는 정리에 대한 부정으로부터 만들어진 각
절에 Ans 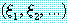 라는 리터럴을 추가하고 하나의 답변 리터럴이 남을 때까지 논리융합을
수행한다. Ans 리터럴의 변수들은, 증명하고자 하는 정리에 대한 부정을 절의 형식으로
표현했을 때 이 절에 나타난 것들이다. 질의에 대한 답변 추출 과정은 [Green 1969b]
에 의해 개발되었다. [Luckham & Nilsson 1971] 은 후에 이 과정에 대한 분석
및 확장을 하였다.
라는 리터럴을 추가하고 하나의 답변 리터럴이 남을 때까지 논리융합을
수행한다. Ans 리터럴의 변수들은, 증명하고자 하는 정리에 대한 부정을 절의 형식으로
표현했을 때 이 절에 나타난 것들이다. 질의에 대한 답변 추출 과정은 [Green 1969b]
에 의해 개발되었다. [Luckham & Nilsson 1971] 은 후에 이 과정에 대한 분석
및 확장을 하였다.

그림 2 답변추출
그림 2 는 Ans 리터럴이 어떻게 사용되었는가를
보여 주는 예이다. 이 예에서 (∃u)I(A, u) 와 같은 정형식을 증명한다. 이 정형식은
로봇이 "어느 방에 A 가 있느냐" 라고 자문하는 것으로 볼 수 있다.
지식베이스내의 식에 사용되는 관계상수는 의도한
의미 (즉, 관계) 를 가지고 있는 것이 보통이다. 그런데 이러한 관계는 관계상수를
표현하는 데 사용된 기호가 아니라 지식베이스의 모델 집합에 의해서 제약을 받는다.
논리융합 반박의 결과는 지식베이스가 실제 관계를 적절히 제약할 때에만 의도한
의미와 양립할 것이다.
그러나 공통적으로 나타나는 중요한 관계가 있다.
예를 들어 동등 관계 (equality relation) 란 것이 있다. 이러한 관계를 나타내는
데 사용되는 관계상수는 Equals (A, B) 와 같은 형이나 A = B 와 같이 중위 (infix)
형으로 사용된다. 지식베이스에 Equals (A, B) 와 같은 식이 포함되어 있다고 해서
P(A) 로부터 P(B) 라는 결론을 내릴 수 있다는 것은 아니다. 또한 Q(A, B) 와 ¬Q(B,
A) 를 논리융합할 수 있는 것도 아니다. 지식베이스는 추가식이 없는 한 Equals 가
무엇을 의미하는지 알 길이 없다.
동등 관계는 다음과 같은 성질을 지닌다.
- 반사성 (reflexive) (∀x) Equals (x, x)
- 대칭성 (symmetric) (∀x, y) [Equals (x,
y) ⊃ Equals (y, x)]
- 이행성 (transitive) (∀x, y, z) [Equals
(x, y) ∧ Equals (y, z) ⊃ Equals (x, z)]
이러한 성질을 이용하더라도 우리는 P(A) 와 Equals
(A, B) 로부터 P(B) 를 증명할 수 없다. 필요한 것은 어떤 식에서든지 같은 항을
같은 항으로 치환할 수 있다는 것이다. 이러한 치환이 가능하려면 지식베이스는 (각
술어상수와 함수상수에 대하여) 허용된 모든 치환을 명시적으로 나열할 수 있어야
한다. 그러나 이러한 요구조건은 현실성이 없다.
몇 가지 현실성 있는 대안이 있는데 그 중 가장
강력한 것은 paramodulation 이다 [Wos & Robinson 1968], [Chang & Lee
1973, pp.168-170]. paramodulation 은 지식베이스에 동등술어가 포함된 경우 논리융합을
하는데 사용되는 동등 관계에 국한된 추론규칙이다. 이것은 다음과 같이 정의된다.
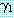 과
과 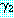 를 각각 리터럴의 집합으로 표현된 절이라고 하자.
를 각각 리터럴의 집합으로 표현된 절이라고 하자. 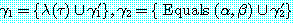 이고 (여기서
이고 (여기서 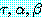 는 항을
는 항을 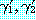 는 절을 그리고
는 절을 그리고 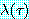 는 항
는 항 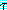 를 포함하고 있는 리터럴이다)
를 포함하고 있는 리터럴이다) 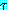 와
와 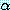 가 mgu
가 mgu 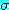 를 가지고 있다면
를 가지고 있다면 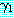 과
과 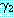 의 이진 paramodulant 를 다음과 같이 추론한다.
의 이진 paramodulant 를 다음과 같이 추론한다.
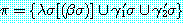
여기서 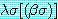 는
는 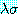 에서
에서 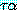 를
를 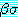 로 대치한 결과를 나타낸다 (동등 관계의 대칭성은
로 대치한 결과를 나타낸다 (동등 관계의 대칭성은 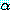 와
와 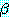 의 역할을 뒤집는 규칙에 의해 처리된다).
의 역할을 뒤집는 규칙에 의해 처리된다).
위 규칙은 매우 복잡해 보이지만 실제로 이것을
적용하는 과정은 그다지 복잡하지 않다. 예를 들어 P(A) 와 (A = B) 로부터 P(B)
를 증명해 보자. 반박을 이용한 증명을 할 때에는 세 개의 절 ¬P(B), P(A), (A =
B) 로부터 공절을 추론해야 한다. 마지막 두 절에 대한 paramodulation 에 의해 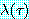 는 P(A) 이며
는 P(A) 이며 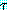 는 A 이고
는 A 이고 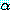 는 A 이며
는 A 이며 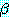 는 B 이다. (
는 B 이다. (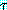 의 역할을 하는) A 와 (
의 역할을 하는) A 와 (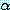 의 역할을 하는) A 는 별도의 치환없이 단일화가 가능하므로 이진 paramodulant
는
의 역할을 하는) A 는 별도의 치환없이 단일화가 가능하므로 이진 paramodulant
는 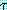 (즉, A) 를
(즉, A) 를 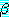 (즉, B) 로 대치한 결과인 P(B) 이다. 이 paramodulant 와 ¬P(B) 를 논리융합하면
공절을 얻게 된다.
(즉, B) 로 대치한 결과인 P(B) 이다. 이 paramodulant 와 ¬P(B) 를 논리융합하면
공절을 얻게 된다.
[Chang & Lee 1973, p.170] 에서 발췌한 다음
예에 위 과정을 적용하면 P(g(f(x))) ∨ Q(x) 와 [f(g(B)) = A] ∨ R(g(c)) 의 이진
paramodulant 는 P(g(A)) ∨ Q(g(B)) ∨ R(g(C)) 이다.
paramodulant 를 조금만 확장하면 논리융합 반박과
결합된 paramodulation 은 동등 술어를 포함하고 있는 지식베이스에 있어서 완전함을
보일 수 있다.
동등 관계끼리 치환하는 것을 요구하지 않는 문제의
경우에는 parmodulation 이 필요하지 않다. 외부 처리를 통해 동등 술어에 대한 진리값을
구할 수 있다면 이 술어를 T 또는 F 중 적당한 값으로 대치할 수 있다. 논리융합
반박에서 T 라는 리터럴을 포함하고 있는 절은 제거할 수 있다. 어떤 절에서든지
F 라는 리터럴은 제거할 수 있다.
예를 들어 짐꾸러미 A 가 R1 이라는 방에 있으면
이 짐꾸러미는 R2 라는 방에 있을 수 없다는 것을 증명하는 문제를 생각해 보자.
로봇의 지식베이스에는 다음과 같은 것이 들어 있을 것이다.
(∀x, y, u, v)[In(x, u) ∧ (u ≠ v)] ⊃
¬In(x, v)
In(A, R1)
.
.
.
이 로봇이 ¬In(A, R2) 를 증명하려고 한다. 첫번째
식을 절로 변환하면 다음과 같다.
¬In(x, u) ∨ (u = v) ∨ ¬In(x, v)
동등 술어가 기초 항만을 가질 때까지 동등 술어에
대한 처리를 연기한다. 증명하고자 하는 정형식의 부정과 이 절을 논리융합하면 다음과
같다.
이것을 주어진 정형식 In(A, R1) 과 논리융합하면
결과는 다음과 같다.
(R2 = R1)
지식베이스에 ¬(R2 = R1) 이라는 정형식이 포함되어
있다고 하자. 이것에 의해 공절이 생성되므로 반박이 끝나게 된다. 그러나 M 개의
방이 있는 대형 빌딩의 경우에는 M(M-1)/2 개의 동등 관계가 필요할 것이다. 그리고
로봇이 숫자와 관련된 추론을 해야 하는 경우에는 ¬(3742 = 4861) 등과 같은 수도
없이 많은 정형식이 필요할 것이다. 이것들을 모두 지식베이스에 명시적으로 저장하는
대신 모든 (기초) 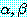 에 대하여
에 대하여 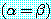 와 같은 형태의 식을 계산할 수 있는 루틴 (즉, 프로그램) 을 제공하는 것이
더 좋을 것이다. 위의 예에 대하여 이 루틴을 수행하면 F (또는 Nil) 를 반환하고
반박이 종료될 것이다.
와 같은 형태의 식을 계산할 수 있는 루틴 (즉, 프로그램) 을 제공하는 것이
더 좋을 것이다. 위의 예에 대하여 이 루틴을 수행하면 F (또는 Nil) 를 반환하고
반박이 종료될 것이다.
흔히 사용되는 관계나 함수 (예를 들면 크다, 작다
등과 같은 관계나, 더하기, 빼기, 나누기 등과 같은 함수) 에 대해서는 추론을 하지
않고 직접 계산을 할 수도 있다. 자동 추론 시스템에서 효율을 증대하기 위한 도구로써
이러한 방법이 사용된다.
어떤 사람들은 논리융합 추론 규칙을 비직관적이라고
생각하고 대신 소위 자연 연역추론 (natural deduction) 방법 [Prawitz 1965 (Prawitz,
D., Natural Deduction: A Proof Theoretical Study, Stockholm: Almquist
and Wiksell, 1965.)] 을 더 선호하였다. 이 방법에서는 주어진 문장을 정규형으로
변형하지 않은 상태에서 추론을 하기 때문에 "자연" 이란 말을 붙인 것이다.
[Bledsoe 1977 (Bledsoe, W., "Non-Resolution Theorem~Proving," Artificial
Intelligence, 9(1):1-35, 1977.)] 에서는 이와 같이 논리융합을 하지 않는 추론
방법에 대하여 논의를 하였다.
Larry Wos 와 Woody Bledsoe 는 논리융합과 그
밖의 다른 추론 방법을 수학에서 나오는 여러 가지 정리를 증명하는 문제에 적용한
선두주자였다. 이들의 연구 결과로 지원 집합 (support set) [Wos, Carson &
Robinson 1965 (Wos, L., Carson, D., and Robinson, G., "Efficiency and Completeness
of the Set-of-Support Strategy in Theorem~Proving," Journal of the Association
for Computing Machinery, 12:536-541, 1965.)] 이나 유닛우선 (unit preference)
과 같은 새로운 논리융합 방법들이 제시되었다. [Wos & Winker 1983 (Wos, L.,
and Winker, S., "Open Questions Solved with the Assistance of AURA,"
in Bledsoe, W., and Loveland, D. (eds.), Automated Theorem Proving: After
25 Years: Proceedings of the Special Session of the 89th Annual Meeting of the
American Mathematical Society, pp.71-88, Denver, Colorado: American Mathematical
Society, 1983.), Boyer & Moore 1979 (Boyer, R., and Moore, J., A Computational
Logic, New York: Academic Press, 1979.) , Stickel 1988 (Stickel, M.,
"A PROLOG Technology Theorem~Prover: Implementation by an Extended
PROLOG Compiler," Journal of Automated Reasoning, 4:353-380,
1988.), McCune 1994 (McCune, W., OTTER 3.0 Reference Manual and Guide,
Technical Report ANL-94/6, Argonne National Laboratory, Argonne, IL, 1994.),
Wos 1993 (Wos, L., "Automated Reasoning Answers Open Questions," Notices
of the AMS, 5(1):15-26, January 1993.)] 에서 강력한 정리증명 시스템들의
예를 볼 수 있다. 이들 시스템 중 일부는 수학에서 미제로 남아있던 정리 문제들을
해결하기도 하였다. [Wos, et al. 1992 (Wos, L., Overbeek, R., Lusk, E., and Boyle,
J., Automated Reasoning: Introduction and Applications, second edition,
New York: McGraw-Hill, 1992.)] 는 컴퓨터에 의한 정리증명 및 이것을 문제 해결에
응용한 내용을 다룬 대표적인 교재이다.
주어진 명세를 충족시키는 프로그램을 작성하고
이것을 검증하는 데에 컴퓨터에 의한 정리증명을 적용해 보기도 하였다. [Manna &
Waldinger 1992 (Manna, Z., and Waldinger, R., "Fundamentals of Deductive
Program~Synthesis," IEEE Transactions on Software Engineering, 18(8):674-704,
1992.)] 에서는 컴퓨터를 이용한 자동 프로그램 제작에 대한 소개를 하고 있다. [Manna
& Waldinger 1985 (Manna, Z., and Waldinger, R., The Logical Basis for
Computer Programming, Volume 1: Deductive Reasoning, Reading, MA: Addison-Wesley,
1985.), Manna & Waldinger 1990 (Manna, Z., and Waldinger, R., The Logical
Basis for Computer Programming, Volume 2: Deductive Systems, Reading, MA:
Addison-Wesley, 1990.)] 은 논리와 프로그래밍에 대하여 자세히 다룬 책이다. [Lowry
& McCartney 1991 (Lowry, M., and McCartney, R., Automating Software Design,
Cambridge, MA: MIT Press, 1991.)] 은 프로그램 제작에 대한 글을 모아둔 책이다.
술어 계산 (predicate evaluation) 은 자료 구조와
프로그램이 술어논리 언어의 구성요소와 연관되어 있는 소위 의미부여 (semantic
attachment) 라고 하는 보다 일반적인 방법의 한 예이다. 부여된 구조와 프로시저는
의도하는 해석과 일치하는 방법으로 그런 언어로 표현된 식들을 계산하는데 사용될
수 있다 [Weyhrauch 1980 (Weyhrauch, R., "Prolegomena to a Theory of Mechanized
Formal Reasoning," Artificial Intelligence, 13(1-2):133-170, 1980.),
Myers 1994 (Myers, K., "Hybrid Reasoning Using Universal Attachment,"
Artificial Intelligence, (67)2:329-375, 1994.)].
Journal of Automated Reasoning 이란 논문은
정리증명 기술에 관한 이론적인 부분과 이의 응용에 대해 다루고 있다.
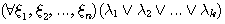 와 같은 정형식을
와 같은 정형식을 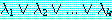 로 줄여서 표현할 때도 있는데 여기서
로 줄여서 표현할 때도 있는데 여기서 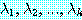 는 변수
는 변수 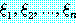 을 포함하고 있는 리터럴을 나타낸다. 이와 같이 전체 한정사를 생략하고 표현하는
경우에
을 포함하고 있는 리터럴을 나타낸다. 이와 같이 전체 한정사를 생략하고 표현하는
경우에 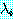 에서 사용된 변수는 전체 한정사에 의해 한정을 받는 것으로 가정한다 (이렇게
하기 위해서는 존재 한정사에 의해 한정받는 변수들을 먼저 제거해야 하는데 이에
대해서는 뒤에서 설명하기로 한다). 이와 같이 간단하게 표현한 정형식을 절 (clause)
이라고 한다. 하나의 절을
에서 사용된 변수는 전체 한정사에 의해 한정을 받는 것으로 가정한다 (이렇게
하기 위해서는 존재 한정사에 의해 한정받는 변수들을 먼저 제거해야 하는데 이에
대해서는 뒤에서 설명하기로 한다). 이와 같이 간단하게 표현한 정형식을 절 (clause)
이라고 한다. 하나의 절을 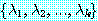 와 같은 집합형식으로 표현하기도 하는데 이런 경우 각 원소들이 논리합으로
연결되어 있는 것으로 가정한다.
와 같은 집합형식으로 표현하기도 하는데 이런 경우 각 원소들이 논리합으로
연결되어 있는 것으로 가정한다.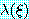 란 리터럴이 포함되어 있고 (ξ 는 변수임), 또 다른 절에 ¬λ(τ) 란 상반된
리터럴이 포함되어 있으며, τ 가 ξ 를 포함하지 않는 항이면, 첫번째 절에서 ξ
를 τ 로 치환한 후 상반된 리터럴에 대한 명제논리에서의 논리융합을 수행함으로써
두 절에 대한 논리융합식 (resolvent) 을 생성할 수 있다.
란 리터럴이 포함되어 있고 (ξ 는 변수임), 또 다른 절에 ¬λ(τ) 란 상반된
리터럴이 포함되어 있으며, τ 가 ξ 를 포함하지 않는 항이면, 첫번째 절에서 ξ
를 τ 로 치환한 후 상반된 리터럴에 대한 명제논리에서의 논리융합을 수행함으로써
두 절에 대한 논리융합식 (resolvent) 을 생성할 수 있다.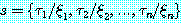 과 같은 순서쌍의 집합으로 나타낼 수도 있다. 순서쌍
과 같은 순서쌍의 집합으로 나타낼 수도 있다. 순서쌍 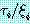 는 치환이 미치는 범위내에 있는 변수
는 치환이 미치는 범위내에 있는 변수 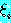 모두를 항
모두를 항 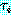 로 바꾸는 것을 의미한다. 어떤 변수를 치환할 때 같은 변수를 포함하고 있는
항과 치환할 수는 없다. 위의 P[x, f(y), B] 에 대한 치환 사례를 얻는 데 사용된
치환은 다음과 같다.
로 바꾸는 것을 의미한다. 어떤 변수를 치환할 때 같은 변수를 포함하고 있는
항과 치환할 수는 없다. 위의 P[x, f(y), B] 에 대한 치환 사례를 얻는 데 사용된
치환은 다음과 같다.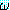 를 s 로 치환한 치환 사례를
를 s 로 치환한 치환 사례를 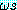 와 같이 표기하기로 한다. 그러므로 P[z, f(w), B] 는 P[x, f(y), B]s1 과 같다.
s1 과 s2 에 대한 합성은 s1s2 로 표기하는데 이것은 s1 의 각 항에 s2 를 적용하고
여기에 s1 에서 나타나지 않고 s2 에서만 나타난 변수를 추가하여 만든 치환을 의미한다.
그러므로 {g(x, y)/z}{A/x, B/y, C/w, D/z} 은 {g(A, B)/z, A/x, B/y, C/w} 와 같다.
어떤 식
와 같이 표기하기로 한다. 그러므로 P[z, f(w), B] 는 P[x, f(y), B]s1 과 같다.
s1 과 s2 에 대한 합성은 s1s2 로 표기하는데 이것은 s1 의 각 항에 s2 를 적용하고
여기에 s1 에서 나타나지 않고 s2 에서만 나타난 변수를 추가하여 만든 치환을 의미한다.
그러므로 {g(x, y)/z}{A/x, B/y, C/w, D/z} 은 {g(A, B)/z, A/x, B/y, C/w} 와 같다.
어떤 식 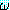 에 s1 과 s2 를 연속해서 적용하는 것은
에 s1 과 s2 를 연속해서 적용하는 것은 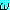 에 s1s2 를 적용하는 것과 같다. 따라서
에 s1s2 를 적용하는 것과 같다. 따라서 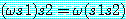 의 관계가 성립한다. 치환 합성은 결합 법칙이 성립한다. 따라서 (s1s2)s3 =
s1(s2s3) 의 관계가 성립한다.
의 관계가 성립한다. 치환 합성은 결합 법칙이 성립한다. 따라서 (s1s2)s3 =
s1(s2s3) 의 관계가 성립한다.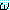 를 P(x, y), s1 을 {f(y)/x}, s2 를 {A/y} 라고 하자. 그러면
를 P(x, y), s1 을 {f(y)/x}, s2 를 {A/y} 라고 하자. 그러면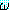 s1)s2 = [P(f(y), y)]{A/y} = P(f(A), A)
s1)s2 = [P(f(y), y)]{A/y} = P(f(A), A) (s1s2) = [P(x, y)]{f(A)/x, A/y} = P(f(A), A)
(s1s2) = [P(x, y)]{f(A)/x, A/y} = P(f(A), A) , s1, s2 를 여기서도 사용한다.)
, s1, s2 를 여기서도 사용한다.) (s1s2) = P(f(A), A)
(s1s2) = P(f(A), A) (s2s1) = [P(x, y)]{A/y, f(y)/x} = P(f(y), A)
(s2s1) = [P(x, y)]{A/y, f(y)/x} = P(f(y), A)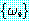 의 모든 원소에 대하여 치환 s 를 적용하는 경우에는 이것을
의 모든 원소에 대하여 치환 s 를 적용하는 경우에는 이것을 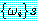 로 표기하기로 한다.
로 표기하기로 한다. 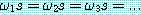 의 관계가 성립하는 치환 s 가 존재하는 경우 정형식의 집합
의 관계가 성립하는 치환 s 가 존재하는 경우 정형식의 집합 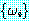 는 단일화가 가능하다 (unifiable) 고 한다. 이러한 경우 치환 s 를
는 단일화가 가능하다 (unifiable) 고 한다. 이러한 경우 치환 s 를 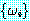 의 단일자 (unifier) 라고 한다. 예를 들어, 치환 s = {A/x, B/y} 는 정형식의
집합 {P[x, f(y), B], P[x, f(B), B]} 를 {P[A, f(B), B]} 로 단일화한다. 비록 치환
s = {A/x, B/y} 는 정형식의 집합 {P[x, f(y), B], P[x, f(B), B]} 에 대한 단일자이지만
이것이 가장 간단한 형태의 단일자는 아니다. 예를 들어, 위에서 x 를 A 로 치환하지
않더라도 단일화를 할 수 있다. 정형식의 집합
의 단일자 (unifier) 라고 한다. 예를 들어, 치환 s = {A/x, B/y} 는 정형식의
집합 {P[x, f(y), B], P[x, f(B), B]} 를 {P[A, f(B), B]} 로 단일화한다. 비록 치환
s = {A/x, B/y} 는 정형식의 집합 {P[x, f(y), B], P[x, f(B), B]} 에 대한 단일자이지만
이것이 가장 간단한 형태의 단일자는 아니다. 예를 들어, 위에서 x 를 A 로 치환하지
않더라도 단일화를 할 수 있다. 정형식의 집합 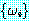 의 가장 일반적인 (또는 가장 단순한) 단일자 (most general unifier, mgu 라고
함) g 는 다음과 같은 성질을 가지고 있다. 치환 s 에 의해 정형식의 집합
의 가장 일반적인 (또는 가장 단순한) 단일자 (most general unifier, mgu 라고
함) g 는 다음과 같은 성질을 가지고 있다. 치환 s 에 의해 정형식의 집합 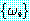 가
가 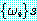 로 단일화되면
로 단일화되면  의 관계가 성립하는 치환 s' 이 존재한다. 또한 가장 일반적인 단일자에 의해
생성된 치환 결과는 알파벳 변이를 제외하고는 유일하다.
의 관계가 성립하는 치환 s' 이 존재한다. 또한 가장 일반적인 단일자에 의해
생성된 치환 결과는 알파벳 변이를 제외하고는 유일하다.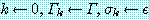 (초기화 단계 :
(초기화 단계 : 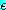 은 공치환 (empty substitution) 을 나타낸다.)
은 공치환 (empty substitution) 을 나타낸다.)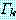 가 하나의 정형식인 경우에는
가 하나의 정형식인 경우에는 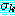 로 단일화가 종료된다. 이 때
로 단일화가 종료된다. 이 때 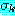 는 Γ 에 대한 mgu 가 된다. 그렇지 않은 경우에는 단일화를 계속한다.
는 Γ 에 대한 mgu 가 된다. 그렇지 않은 경우에는 단일화를 계속한다.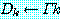 에 대한 불일치 집합
에 대한 불일치 집합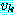 는
는 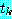 에 나타나지 않는 변수라고 하자. 이러한 조건을 만족하는 변수
에 나타나지 않는 변수라고 하자. 이러한 조건을 만족하는 변수 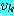 와
와 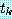 가
가 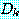 에 존재하는 경우에는 단일화를 계속한다. 그렇지 않은 경우에는 단일화가 실패된
것으로 보고 단일화를 종료한다. 즉, 이러한 경우 Γ 는 단일화할 수 없다.
에 존재하는 경우에는 단일화를 계속한다. 그렇지 않은 경우에는 단일화가 실패된
것으로 보고 단일화를 종료한다. 즉, 이러한 경우 Γ 는 단일화할 수 없다.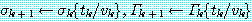 (
(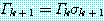 임에 주의하라.)
임에 주의하라.)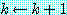
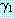 과
과 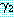 를 각각 리터럴의 집합으로 표현된 절이라고 하자.
를 각각 리터럴의 집합으로 표현된 절이라고 하자. 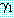 에 아톰
에 아톰 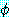 가 있고
가 있고 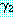 에 리터럴
에 리터럴 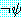 가 있을 때
가 있을 때 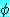 와
와 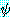 가 mgu
가 mgu 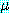 를 가지고 있다면 이 두 절은 논리융합식
를 가지고 있다면 이 두 절은 논리융합식 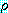 를 가진다. 논리융합식은
를 가진다. 논리융합식은 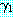 과
과 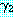 의 합집합에 치환
의 합집합에 치환 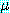 를 적용함으로써 얻어진다. 즉,
를 적용함으로써 얻어진다. 즉, 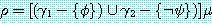
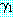 과
과 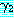 를 각각 리터럴의 집합으로 표현한 절이라고 하자.
를 각각 리터럴의 집합으로 표현한 절이라고 하자. 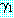 과
과 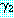 를 각각
를 각각 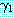 ,
, 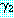 의 부분집합이라고 했을 때 mgu
의 부분집합이라고 했을 때 mgu 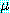 를 사용하여
를 사용하여 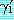 의 리터럴들과
의 리터럴들과 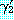 의 리터럴들의 부정을 단일화시킬 수 있다면 이 두 절은 논리융합식
의 리터럴들의 부정을 단일화시킬 수 있다면 이 두 절은 논리융합식 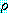 를 가진다. 이 논리융합식은
를 가진다. 이 논리융합식은 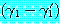 과
과 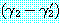 의 합집합에 치환
의 합집합에 치환 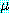 를 적용함으로써 얻어진다. 즉,
를 적용함으로써 얻어진다. 즉,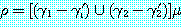
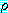 가 두 절
가 두 절 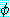 와
와 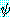 의 논리융합식이라면
의 논리융합식이라면 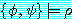 이다. 이것을 증명하는 것은 명제논리에서의 논리융합에 대한 정당성 (soundness)
을 증명하는 것보다 어렵지 않다. 논리융합만으로는 주어진 정형식의 집합으로부터
논리적으로 귀결 (logically entail) 되는 모든 식을 추론할 수 없다. 예를 들어,
P(A) 로부터 P(A) ∨ P(B) 를 추론할 수 없다. 명제논리에서의 논리융합에서는 논리융합
반박 (resolution refutation) 을 이용하여 이러한 문제점을 극복하였는데 술어논리에서도
마찬가지로 할 수 있다. 그러나 반박의 완전성 (completeness) 을 보장하기 위해서는
논리융합에 대한 보다 강력한 정의를 이용해야 한다.
이다. 이것을 증명하는 것은 명제논리에서의 논리융합에 대한 정당성 (soundness)
을 증명하는 것보다 어렵지 않다. 논리융합만으로는 주어진 정형식의 집합으로부터
논리적으로 귀결 (logically entail) 되는 모든 식을 추론할 수 없다. 예를 들어,
P(A) 로부터 P(A) ∨ P(B) 를 추론할 수 없다. 명제논리에서의 논리융합에서는 논리융합
반박 (resolution refutation) 을 이용하여 이러한 문제점을 극복하였는데 술어논리에서도
마찬가지로 할 수 있다. 그러나 반박의 완전성 (completeness) 을 보장하기 위해서는
논리융합에 대한 보다 강력한 정의를 이용해야 한다. (∃x)P(x) 가 성립하지만 [P(A) ∨ P(B)]
(∃x)P(x) 가 성립하지만 [P(A) ∨ P(B)] 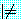 P(Sk) 는 성립하지 않는다. 정형식의 집합 Δ 은 Δ 의 Skolem 형식이 만족 가능할
때에 한하여 만족 가능하다고 한다. 또는 Δ 의 Skolem 형식이 만족 불가능할
때에 한하여 Δ 는 만족 불가능 (unsatisfiable) 하다고 한다 [Loveland 1978,
pp.41ff].
P(Sk) 는 성립하지 않는다. 정형식의 집합 Δ 은 Δ 의 Skolem 형식이 만족 가능할
때에 한하여 만족 가능하다고 한다. 또는 Δ 의 Skolem 형식이 만족 불가능할
때에 한하여 Δ 는 만족 불가능 (unsatisfiable) 하다고 한다 [Loveland 1978,
pp.41ff].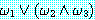 을
을 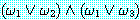 로 대치하는 분배 법칙을 계속 적용함으로써 논리곱 정규형으로 변형된다.
로 대치하는 분배 법칙을 계속 적용함으로써 논리곱 정규형으로 변형된다.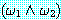 형식으로 주어진 식을 정형식의 집합
형식으로 주어진 식을 정형식의 집합 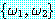 로 대치함으로써 논리곱 기호를 제거할 수 있다. 이러한 절차를 반복하면 정형식의
유한집합을 얻을 수 있다. 여기서 각 정형식은 리터럴의 논리곱이다. 리터럴들의
논리합만으로 이루어진 정형식을 절 (clause) 이라고 불린다. 이 책에서 예로
든 정형식은 다음과 같은 절의 집합으로 변형된다.
로 대치함으로써 논리곱 기호를 제거할 수 있다. 이러한 절차를 반복하면 정형식의
유한집합을 얻을 수 있다. 여기서 각 정형식은 리터럴의 논리곱이다. 리터럴들의
논리합만으로 이루어진 정형식을 절 (clause) 이라고 불린다. 이 책에서 예로
든 정형식은 다음과 같은 절의 집합으로 변형된다.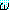 가 정형식의 집합 Δ 로부터 논리적으로 유도된다면 정형식
가 정형식의 집합 Δ 로부터 논리적으로 유도된다면 정형식 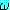 는 Δ 에 속한 정형식을 절로 변형하여 얻은 절의 집합으로부터도 논리적으로
유도되며 역도 성립한다 [Davis & Putnam 1960]. 따라서 절은 술어논리에서의
정형식을 표현하는 일반적인 형식이다.
는 Δ 에 속한 정형식을 절로 변형하여 얻은 절의 집합으로부터도 논리적으로
유도되며 역도 성립한다 [Davis & Putnam 1960]. 따라서 절은 술어논리에서의
정형식을 표현하는 일반적인 형식이다. 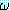 을 증명하는 것은 명제논리에서의 증명방법과 같다. 즉,
을 증명하는 것은 명제논리에서의 증명방법과 같다. 즉, 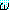 를 부정한 다음 이것을 절로 변형하고 이것을 Δ 의 절에 추가한다. 그리고 나서
공절이 연역적으로 추론 (deduce) 될 때까지 논리융합을 적용한다. 명제논리에서의
논리융합에 대한 설명을 하면서 소개한 순서 (ordering) 와 개선 전략 (refinement
strategy) 을 사용할 수도 있다.
를 부정한 다음 이것을 절로 변형하고 이것을 Δ 의 절에 추가한다. 그리고 나서
공절이 연역적으로 추론 (deduce) 될 때까지 논리융합을 적용한다. 명제논리에서의
논리융합에 대한 설명을 하면서 소개한 순서 (ordering) 와 개선 전략 (refinement
strategy) 을 사용할 수도 있다. 
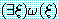 와 같은 형태의 정리를 증명한다고 가정해 보자. 이미 존재하는 것으로 증명된
ξ 를 생성하려 하는 경우도 있을 것이다. 이를 위해서는 반박 과정 중에 적용된
치환을 기억하고 있어야 한다. 이러한 치환은 답변 리터럴 (answer literal) 이라는
형식으로 기억할 수 있다. 증명하고자 하는 정리에 대한 부정으로부터 만들어진 각
절에 Ans
와 같은 형태의 정리를 증명한다고 가정해 보자. 이미 존재하는 것으로 증명된
ξ 를 생성하려 하는 경우도 있을 것이다. 이를 위해서는 반박 과정 중에 적용된
치환을 기억하고 있어야 한다. 이러한 치환은 답변 리터럴 (answer literal) 이라는
형식으로 기억할 수 있다. 증명하고자 하는 정리에 대한 부정으로부터 만들어진 각
절에 Ans 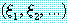 라는 리터럴을 추가하고 하나의 답변 리터럴이 남을 때까지 논리융합을
수행한다. Ans 리터럴의 변수들은, 증명하고자 하는 정리에 대한 부정을 절의 형식으로
표현했을 때 이 절에 나타난 것들이다. 질의에 대한 답변 추출 과정은 [Green 1969b]
에 의해 개발되었다. [Luckham & Nilsson 1971] 은 후에 이 과정에 대한 분석
및 확장을 하였다.
라는 리터럴을 추가하고 하나의 답변 리터럴이 남을 때까지 논리융합을
수행한다. Ans 리터럴의 변수들은, 증명하고자 하는 정리에 대한 부정을 절의 형식으로
표현했을 때 이 절에 나타난 것들이다. 질의에 대한 답변 추출 과정은 [Green 1969b]
에 의해 개발되었다. [Luckham & Nilsson 1971] 은 후에 이 과정에 대한 분석
및 확장을 하였다.
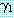 과
과 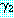 를 각각 리터럴의 집합으로 표현된 절이라고 하자.
를 각각 리터럴의 집합으로 표현된 절이라고 하자. 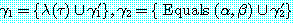 이고 (여기서
이고 (여기서 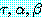 는 항을
는 항을 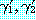 는 절을 그리고
는 절을 그리고 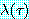 는 항
는 항 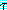 를 포함하고 있는 리터럴이다)
를 포함하고 있는 리터럴이다) 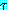 와
와 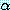 가 mgu
가 mgu 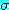 를 가지고 있다면
를 가지고 있다면 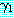 과
과 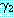 의 이진 paramodulant 를 다음과 같이 추론한다.
의 이진 paramodulant 를 다음과 같이 추론한다.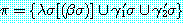
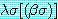 는
는 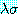 에서
에서 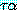 를
를 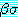 로 대치한 결과를 나타낸다 (동등 관계의 대칭성은
로 대치한 결과를 나타낸다 (동등 관계의 대칭성은 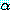 와
와 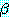 의 역할을 뒤집는 규칙에 의해 처리된다).
의 역할을 뒤집는 규칙에 의해 처리된다).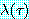 는 P(A) 이며
는 P(A) 이며 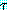 는 A 이고
는 A 이고 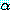 는 A 이며
는 A 이며 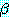 는 B 이다. (
는 B 이다. (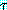 의 역할을 하는) A 와 (
의 역할을 하는) A 와 (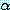 의 역할을 하는) A 는 별도의 치환없이 단일화가 가능하므로 이진 paramodulant
는
의 역할을 하는) A 는 별도의 치환없이 단일화가 가능하므로 이진 paramodulant
는 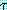 (즉, A) 를
(즉, A) 를 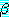 (즉, B) 로 대치한 결과인 P(B) 이다. 이 paramodulant 와 ¬P(B) 를 논리융합하면
공절을 얻게 된다.
(즉, B) 로 대치한 결과인 P(B) 이다. 이 paramodulant 와 ¬P(B) 를 논리융합하면
공절을 얻게 된다.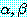 에 대하여
에 대하여 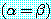 와 같은 형태의 식을 계산할 수 있는 루틴 (즉, 프로그램) 을 제공하는 것이
더 좋을 것이다. 위의 예에 대하여 이 루틴을 수행하면 F (또는 Nil) 를 반환하고
반박이 종료될 것이다.
와 같은 형태의 식을 계산할 수 있는 루틴 (즉, 프로그램) 을 제공하는 것이
더 좋을 것이다. 위의 예에 대하여 이 루틴을 수행하면 F (또는 Nil) 를 반환하고
반박이 종료될 것이다.