 에 대해 다음과 같이
에 대해 다음과 같이 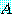 의 고유치를 구한다.
의 고유치를 구한다.Eigenvalue
수치해석 : Kendall Atkinson 저, 김선영 옮김, 희중당, 1994 (원서 : Elementary Numerical Analysis : John Wiley & Sons, 1993), page 286~299
특성다항식 (The Characteristic Polynomial)
대칭행렬의 고유치 (Eigenvalues for Symmetric Matrices)
비 대칭행렬의 고유치문제 (The Nonsymmetric Eigenvalue Problem)
멱방법의 수렴 (Convergence of the Power Method)
정방행렬  에 대해 다음과 같이
에 대해 다음과 같이 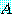 의 고유치를 구한다.
의 고유치를 구한다.
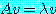 (1)
(1)
이면 이때 수 λ 를 행렬 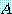 의 고유치 (eigenvalue) 라 하고 행행렬
의 고유치 (eigenvalue) 라 하고 행행렬 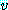 를 고유벡터 (eigenvector) 라고 부른다. 행렬
를 고유벡터 (eigenvector) 라고 부른다. 행렬 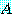 의 고유치-고유벡터
의 고유치-고유벡터 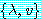 는 선형계
는 선형계 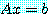 를 풀 때와, 일반 열행렬
를 풀 때와, 일반 열행렬 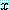 와
와 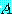 의 곱으로 쓸 때, 또 그 과정을 이해하는 데 쓸 수 있다. 고유치와 고유벡터는
많은 물리문제들을 풀 때 자연적으로 발생한다. 팽팽한 현이나 악기 진동의 자연주파수에서처럼
특정한 기본해를 이끌어내는 것은 초기물리적 흥미거리이다. 이 절에서 고유치와
고유벡터의 정리를 짧게 소개하고 행렬의 최대고유치를 계산하는 수치적 방법을 제시한다.
의 곱으로 쓸 때, 또 그 과정을 이해하는 데 쓸 수 있다. 고유치와 고유벡터는
많은 물리문제들을 풀 때 자연적으로 발생한다. 팽팽한 현이나 악기 진동의 자연주파수에서처럼
특정한 기본해를 이끌어내는 것은 초기물리적 흥미거리이다. 이 절에서 고유치와
고유벡터의 정리를 짧게 소개하고 행렬의 최대고유치를 계산하는 수치적 방법을 제시한다.
예제 행렬
에 대하여 고유치-고유벡터는 각각
이다. (1) 가 위의 두쌍 모두에 대해 만족함을 보일 수 있다. 열행렬
로 쓸 수 있다는 것을 보일 수 있다.
따라서
그림 1 |
식 (1) 의 정의를
 (6)
(6)
으로 다시 써보자. 이것은 계수행렬  와 0 이 아닌 해
와 0 이 아닌 해  를 가지는 선형방정식의 동차 (homogeneous) 계이다. 8.1절의 정리 8.1 로부터
이것은
를 가지는 선형방정식의 동차 (homogeneous) 계이다. 8.1절의 정리 8.1 로부터
이것은
 (7)
(7)
과 서로 동치이다. 이때

을  의 고유 특성다항식 (characteristic polynomial) 이라 부르고, 그것의 해는
의 고유 특성다항식 (characteristic polynomial) 이라 부르고, 그것의 해는
 의 고유치이다. 행렬식의 성질을 이용하여
의 고유치이다. 행렬식의 성질을 이용하여  의 크기를
의 크기를  이라고 가정하면
이라고 가정하면  의 특성다항식은
의 특성다항식은
 (8)
(8)
인 차수  의 다항식이 됨을 보일 수 있다.
의 다항식이 됨을 보일 수 있다.

이다. 식 (8) 은 크기  인 행렬
인 행렬  는 많아야
는 많아야  개의 서로 다른 고유치를 가질 수 있다는 것을 보여준다.
개의 서로 다른 고유치를 가질 수 있다는 것을 보여준다.
예제 식 (2) 의 행렬
이다. 이 다항식의 해 |
일단 고유치가 알려지면 고유벡터  는
는  자리에 실제 고유치를 대입하여 선형계 (6) 을 풀어서 구할 수 있다. 이때
자리에 실제 고유치를 대입하여 선형계 (6) 을 풀어서 구할 수 있다. 이때  의 모든 상수배 또한 해가 되므로 해
의 모든 상수배 또한 해가 되므로 해  는 유일한 것이 아니다. 반올림오차가 생길 수 있기 때문에 해
는 유일한 것이 아니다. 반올림오차가 생길 수 있기 때문에 해 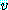 를 구하는 과정은 간단하지 않다. 반올림오차가 없는 간단한 풀이과정을 보기
위해 다음의 예제를 해보자.
를 구하는 과정은 간단하지 않다. 반올림오차가 없는 간단한 풀이과정을 보기
위해 다음의 예제를 해보자.
예제 행렬
이면
해는
이다.
이 된다. 만약 이 계에서
이 되고
혹은 이 벡터의 0 이 아닌 상수배도
고유벡터이다. |
일반적으로 고유치는 고유다항식의 해를 구하는
것으로 구하지 않는다. 같은 고유치를 가지나 공 치계산이 보다 더 쉽게 되는 동치행렬로
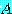 를 변형시켜 구한다. 여기서 이러한 방법을 생각해보지는 않을 것이다. 그러나
좋은 컴퓨터 패키지를 이용하여 쉽게 그러한 과정을 수행할 수 있다.
를 변형시켜 구한다. 여기서 이러한 방법을 생각해보지는 않을 것이다. 그러나
좋은 컴퓨터 패키지를 이용하여 쉽게 그러한 과정을 수행할 수 있다.
행렬 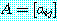 가
가
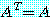
이면 또는
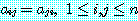
일 때 행렬 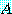 는 대칭행렬이다. 즉,
는 대칭행렬이다. 즉, 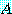 가
가 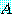 의 대각원소들을 축으로 하여 대칭이 된다는 것을 의미한다.
의 대각원소들을 축으로 하여 대칭이 된다는 것을 의미한다.
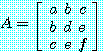
은 크기 3 인 대칭행렬의 일반형이다. 대칭행렬은 주로 응용에서 나타난다. 이 경우 고유치 문제의 수치 해석과 정리 모두 훨씬 간단해진다. 대칭행렬에 대해서는 다음과 같은 중요한 결과가 있다.
정리 정리 1 (i) (ii) 열행렬 (iii) 각각의 열행렬
이 되는 상수
여기서 (iv) 크기
로 정의하면
이고
가 된다. |
이 정리의 증명은 이 장에서 다루지 않았던 선형대수의
개념을 요구하며 상당히 길기 때문에 생략한다. 식 (16) 을 만족하는 행렬을 직교
(orthogonal) 행렬이라 부르고 그것들은 행렬대수문제를 다루는 수치해석에 중요하다.
성질 (16) 은 또한 벡터 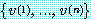 이 길이
이 길이 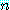 의 모든 열벡터의 벡터공간에 대한 직교기저 (orthogonal basic) 를 이룬다는
것을 말해준다. 그러한 직교 (orthogonal) 행렬의 예로 문제 10 을 보아라. 그리고
8.3 절의 문제 6 을 보아라.
의 모든 열벡터의 벡터공간에 대한 직교기저 (orthogonal basic) 를 이룬다는
것을 말해준다. 그러한 직교 (orthogonal) 행렬의 예로 문제 10 을 보아라. 그리고
8.3 절의 문제 6 을 보아라.
예제 식 (2) 에 있는 행렬
로 바꾸자. 식 (14) 의 행렬
가 되고
|
식 (15) 는 종종
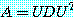 (17)
(17)
로 쓴다. 수학적인 면과 수학외적인 면 모두에서
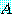 의 이런 분해는 많은 응용에서 유용하다.
의 이런 분해는 많은 응용에서 유용하다.
비 대칭행렬에서 고유치와 고유벡터가 있을 가능성이
더 많다. 특성다항식 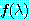 의 근은 복소수가 될 수 있고, 그러면 원소가 복소수인 고유벡터가 된다. 또한
대칭행렬에 대해 식 (12) 에서 했던 것처럼,
의 근은 복소수가 될 수 있고, 그러면 원소가 복소수인 고유벡터가 된다. 또한
대칭행렬에 대해 식 (12) 에서 했던 것처럼, 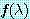 의 다중근 (multiple root) 에 대해 임의의 열행렬
의 다중근 (multiple root) 에 대해 임의의 열행렬 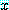 를 고유벡터의 결합으로 쓸 수는 없을 것이다. 그리고 더 이상 (13) 과 같은
계수에 대한 간단한 형식은 없다. 비대칭고유치문제는 중요하다. 그러나 그것은 일반정리에서는
너무 복잡한 문제이기 때문에 여기서는 다루지 않겠다.
를 고유벡터의 결합으로 쓸 수는 없을 것이다. 그리고 더 이상 (13) 과 같은
계수에 대한 간단한 형식은 없다. 비대칭고유치문제는 중요하다. 그러나 그것은 일반정리에서는
너무 복잡한 문제이기 때문에 여기서는 다루지 않겠다.
예제 복소수 고유치가 존재하는 예를 살펴보자.
행렬
이 행렬
이고 이에 대응되는 고유벡터는 다음과 같다.
|
크기가 큰 행렬 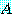 의 고유치를 계산하는 수치적 방법을 설명해 보겠다. 이 과정은 일반적이지는
않으나 프로그램하기 쉽고 많은 행렬에 만족스러운 방법이다. 행렬
의 고유치를 계산하는 수치적 방법을 설명해 보겠다. 이 과정은 일반적이지는
않으나 프로그램하기 쉽고 많은 행렬에 만족스러운 방법이다. 행렬 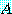 의 고유치
의 고유치 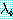 가
가
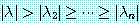 (18)
(18)
를 만족한다는 가정이 필요하다. 여기서 이러한 고유치들은 고유다항식의 근으로서 중복도 만큼 반복될 수도 있다.
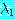 와 이것에 관계된 고유벡터
와 이것에 관계된 고유벡터 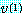 을 계산하기 위한 반복과정을 정의해 보자.
을 계산하기 위한 반복과정을 정의해 보자. 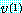 에 대한 초기근사값을 택해 그것을
에 대한 초기근사값을 택해 그것을 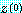 이라고 하자. 일반적으로 난수발생기 (random number generator) 를 사용하여
각 원소를 택하는 방법으로 무작위로 선택된다.
이라고 하자. 일반적으로 난수발생기 (random number generator) 를 사용하여
각 원소를 택하는 방법으로 무작위로 선택된다.

라고 정의하고 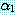 를
를 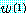 의 최대원소라고 놓자. 만약 그러한 원소가 하나 이상 존재한다면 그러한 원소
중 첫 번째 것을
의 최대원소라고 놓자. 만약 그러한 원소가 하나 이상 존재한다면 그러한 원소
중 첫 번째 것을 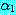 로 선택하자. 그러면
로 선택하자. 그러면
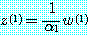
으로 정의할 수 있다. 이 과정을 반복하여
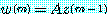 (19)
(19)
로 정의하고 역시 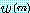 의 최대원소를
의 최대원소를 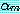 이라 하자.
이라 하자.
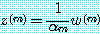 (20)
(20)
라고 정의하면 벡터 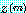 이 대충
이 대충 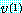 의 곱으로 수렴한다고 말할 수 있다.
의 곱으로 수렴한다고 말할 수 있다.
이런 방법으로 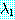 를 찾아내기 위해 벡터
를 찾아내기 위해 벡터 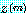 과
과 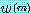 의 0 이 아닌 원소 몇 개를 골라내자. 그것을 원소
의 0 이 아닌 원소 몇 개를 골라내자. 그것을 원소 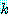 라 하고
라 하고 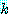 를 고정시키자. 종종 이것이 큰
를 고정시키자. 종종 이것이 큰 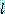 에 대하여
에 대하여 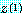 의 최대원소가 된다.
의 최대원소가 된다.  을
을 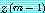 의
의 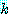 번째 원소라고 하면
번째 원소라고 하면
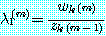 (21)
(21)
로 정의된다. 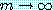 일 때
일 때  은
은 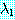 로 수렴함을 보일 수 있다.
로 수렴함을 보일 수 있다.
표 1 (23) 에 대한 멱방법
|
|
|
|
|
|
Ratio |
|
0 1 2 3 4 5 6 7 |
1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 |
0.5 0.8461538 0.9591837 0.9896373 0.9973992 0.9993492 0.9998373 0.9999593 |
1.6250000 1.8846154 1.9693878 1.9922280 1.9982494 1.9995119 1.9998779 |
2.596E-1 8.477E-2 2.284E-2 5.821E-3 1.462E-3 3.660E-4 |
0.327 0.269 0.255 0.251 0.250 |
예제 이 전 예제의 (2) 에 멱방법을 적용시켜 보자.
결과는 표 1 과 같다. |
멱방법의 수렴을 분석하기 위해 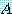 가 대칭행렬일 때만을 생각해 보자. 또 (18) 와 같이
가 대칭행렬일 때만을 생각해 보자. 또 (18) 와 같이 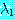 이 최대라고 가정하자.
이 최대라고 가정하자.
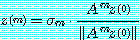 (23)
(23)
우선 위를 보이기로 한다. 여기서 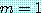 일 때
일 때 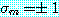 이다.
이다. 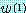 의 최대원소를
의 최대원소를
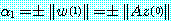
이라 하면
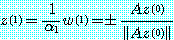
이다. 이 정의에서는 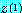 의 최대원소 혹은 크기에서 최대원소가 여러 개 있을 경우 그러한 원소 중 첫
번째 것을 1 이 되게 만든다. 그러므로 우변의 부호는 이에 따라서 선택된다. 식
(23) 의 일반적 경우의 증명은
의 최대원소 혹은 크기에서 최대원소가 여러 개 있을 경우 그러한 원소 중 첫
번째 것을 1 이 되게 만든다. 그러므로 우변의 부호는 이에 따라서 선택된다. 식
(23) 의 일반적 경우의 증명은 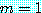 인 경우에서와 같은 아이디어를 사용하여 귀납적으로 할 수 있다. 식 (20) 의
정의에 의해 부호
인 경우에서와 같은 아이디어를 사용하여 귀납적으로 할 수 있다. 식 (20) 의
정의에 의해 부호  은 식 (23) 의 우변의 최대원소가 1 이 되도록 선택한다.
은 식 (23) 의 우변의 최대원소가 1 이 되도록 선택한다.
식 (12) 를 사용하여,
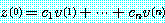 (24)
(24)
로 쓴다. 이때 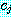 들은 식 (13) 에서 주어진 것이고
들은 식 (13) 에서 주어진 것이고 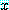 자리에
자리에 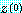 을 쓴 것이다.
을 쓴 것이다. 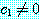 이라고 가정하자. 만약
이라고 가정하자. 만약 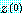 을 무작위로 선택한다면
을 무작위로 선택한다면 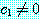 이 된다. 비록
이 된다. 비록 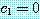 일지라도 오차 때문에 멱방법에서는
일지라도 오차 때문에 멱방법에서는 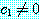 이 된다. 식 (24) 의
이 된다. 식 (24) 의 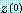 에
에 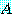 를 곱하면
를 곱하면
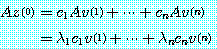
을 얻는다. 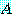 를 계속 곱하면
를 계속 곱하면
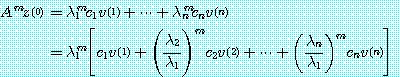
을 얻는다. 식 (23) 으로부터
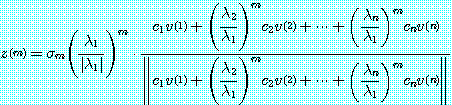 (25)
(25)
이 되고 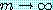 일 때
일 때 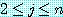 인
인  에 대해서
에 대해서 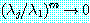 이 되고
이 되고 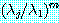 은 최대이다. 또한
은 최대이다. 또한
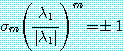
이므로 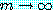 일 때 식 (25) 의 대부분의 항은 0 으로 수렴한다.
일 때 식 (25) 의 대부분의 항은 0 으로 수렴한다. 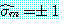 일 때 분자, 분모에서
일 때 분자, 분모에서 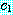 을 소거하여
을 소거하여
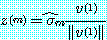
이 되도록 할 수 있다. 만약 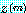 의 정규화 (normalization) 를 항상 몇 개의 특별한 원소가 양수가 되도록 수정한다면
의 정규화 (normalization) 를 항상 몇 개의 특별한 원소가 양수가 되도록 수정한다면
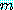 과 관계없는 고정된 부호를 갖고
과 관계없는 고정된 부호를 갖고
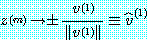 (26)
(26)
이 된다. 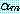 으로 나누어서 부호를 정규화하면 대개 위가 성립한다. 문제 13 을 보아라.
으로 나누어서 부호를 정규화하면 대개 위가 성립한다. 문제 13 을 보아라. 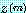 에서 오차는 상수
에서 오차는 상수 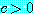 에 대해
에 대해
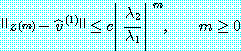 (27)
(27)
를 만족할 것이다.
비슷한 오차의 범위에 대하여 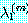 이
이 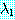 에 수렴하는 것을 보일 때도 위와 같은 분석을 할 수 있다. 또한
에 수렴하는 것을 보일 때도 위와 같은 분석을 할 수 있다. 또한
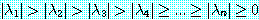 (28)
(28)
를 가정한다면 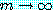 일 때 상수
일 때 상수 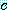 에 대해
에 대해
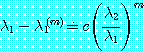 (29)
(29)
라는 것을 볼 수 있다. 예를 들면, 식 (22) 에
있는 행렬 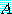 에 대한 표 2 의 계산을 상기해보자.
에 대한 표 2 의 계산을 상기해보자. 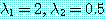 그리고
그리고 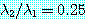 가 된다. 표에 있는 비율은 0.25 에 접근함에 주의하라. 식 (29) 의 결과와 동일함을
알 수 있다.
가 된다. 표에 있는 비율은 0.25 에 접근함에 주의하라. 식 (29) 의 결과와 동일함을
알 수 있다.
표 2 3 차 최소자승법을 위한 데이터
|
|
|
|
|
|
0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.45 0.50 |
0.486 0.866 0.944 1.144 1.103 1.202 1.166 1.191 1.124 1.095 1.122 |
0.55 0.60 0.65 0.70 0.75 0.80 0.85 0.90 0.95 1.00
|
1.102 1.099 1.017 1.111 1.117 1.152 1.265 1.380 1.575 1.857
|
예제 멱방법을 대칭행렬에 적용해보자.
고유치는 각각
이고
이다. 멱방법을 사용한 결과는 표 3 절에서 보여준다.
표 3 (30) 에 대한 멱방법
에 접근함을 주목하라.
|
반복값 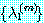 에 대한 오차결과 (29) 은 가속 (acceleration) 방법을 만드는데 사용된다. 식
(29) 에서 충분히 큰
에 대한 오차결과 (29) 은 가속 (acceleration) 방법을 만드는데 사용된다. 식
(29) 에서 충분히 큰 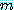 의 모든 값에 대해
의 모든 값에 대해
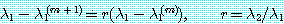 (31)
(31)
가 된다.
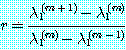 (32)
(32)
을 사용하여  를 선택하자. 이것이 타당한가 하는 것은 문제 14 (d) 에서 보도록 하자. 이런
를 선택하자. 이것이 타당한가 하는 것은 문제 14 (d) 에서 보도록 하자. 이런
 을 이용하여 (31) 의
을 이용하여 (31) 의 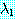 을 구해보자.
을 구해보자.
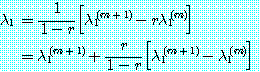 (33)
(33)
이것을 Aitken 유추공식 (extrapolation formula) 이라 한다. 이것을 이용하여 다음과 같은 오차추정값을 구할 수 있는데 이를 Aitken 오차추정공식이라고 한다.
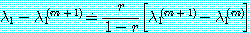 (34)
(34)
가정 (28) 하에서 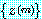 에 대해서 비슷한 결과를 보일 수 있다. Aitken 의 유추법에 관련된 자료는 4.4
절의 근을 찾기 위한 부동점 반복법을 다룰 때 이미 보았다.
에 대해서 비슷한 결과를 보일 수 있다. Aitken 의 유추법에 관련된 자료는 4.4
절의 근을 찾기 위한 부동점 반복법을 다룰 때 이미 보았다.
예제 표 3 에서
이 되고 이것은 실제오차이다. 또한
Aitken 의 공식 (33) 을 이용해 |